Solveeit Logo
Login

Question

Question: If $\int x \sin^{-1}x dx = \frac{2x^2-1}{4}f(x) + \frac{x}{4}g(x) + C$, then:...

If ∫xsin⁡−1xdx=2x2−14f(x)+x4g(x)+C\int x \sin^{-1}x dx = \frac{2x^2-1}{4}f(x) + \frac{x}{4}g(x) + C, then:

Answer

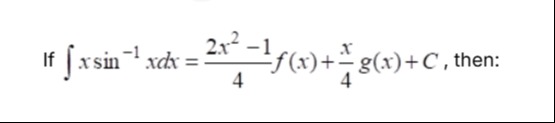
f(x) = arcsin(x), g(x) = √(1-x^2)

Explanation

Solution

To evaluate the integral ∫xsin⁡−1xdx\int x \sin^{-1}x dx, we use integration by parts, which states ∫udv=uv−∫vdu\int u dv = uv - \int v du.

Let u=sin⁡−1xu = \sin^{-1}x and dv=xdxdv = x dx. Then, we find dudu and vv: du=ddx(sin⁡−1x)dx=11−x2dxdu = \frac{d}{dx}(\sin^{-1}x) dx = \frac{1}{\sqrt{1-x^2}} dx v=∫xdx=x22v = \int x dx = \frac{x^2}{2}

Now, substitute these into the integration by parts formula: ∫xsin⁡−1xdx=x22sin⁡−1x−∫x22⋅11−x2dx\int x \sin^{-1}x dx = \frac{x^2}{2} \sin^{-1}x - \int \frac{x^2}{2} \cdot \frac{1}{\sqrt{1-x^2}} dx =x22sin⁡−1x−12∫x21−x2dx= \frac{x^2}{2} \sin^{-1}x - \frac{1}{2} \int \frac{x^2}{\sqrt{1-x^2}} dx

Next, we need to evaluate the integral I1=∫x21−x2dxI_1 = \int \frac{x^2}{\sqrt{1-x^2}} dx. We can rewrite the numerator x2x^2 as −(1−x2)+1-(1-x^2) + 1: I1=∫1−(1−x2)1−x2dx=∫(11−x2−1−x21−x2)dxI_1 = \int \frac{1-(1-x^2)}{\sqrt{1-x^2}} dx = \int \left( \frac{1}{\sqrt{1-x^2}} - \frac{1-x^2}{\sqrt{1-x^2}} \right) dx I1=∫(11−x2−1−x2)dxI_1 = \int \left( \frac{1}{\sqrt{1-x^2}} - \sqrt{1-x^2} \right) dx We know the standard integral formulas: ∫1a2−x2dx=sin⁡−1(xa)\int \frac{1}{\sqrt{a^2-x^2}} dx = \sin^{-1}\left(\frac{x}{a}\right) ∫a2−x2dx=x2a2−x2+a22sin⁡−1(xa)\int \sqrt{a^2-x^2} dx = \frac{x}{2}\sqrt{a^2-x^2} + \frac{a^2}{2}\sin^{-1}\left(\frac{x}{a}\right)

For a=1a=1: ∫11−x2dx=sin⁡−1x\int \frac{1}{\sqrt{1-x^2}} dx = \sin^{-1}x ∫1−x2dx=x21−x2+12sin⁡−1x\int \sqrt{1-x^2} dx = \frac{x}{2}\sqrt{1-x^2} + \frac{1}{2}\sin^{-1}x Substitute these back into I1I_1: I1=sin⁡−1x−(x21−x2+12sin⁡−1x)I_1 = \sin^{-1}x - \left( \frac{x}{2}\sqrt{1-x^2} + \frac{1}{2}\sin^{-1}x \right) I1=sin⁡−1x−x21−x2−12sin⁡−1xI_1 = \sin^{-1}x - \frac{x}{2}\sqrt{1-x^2} - \frac{1}{2}\sin^{-1}x I1=12sin⁡−1x−x21−x2I_1 = \frac{1}{2}\sin^{-1}x - \frac{x}{2}\sqrt{1-x^2}

Now, substitute I1I_1 back into the main integral expression: ∫xsin⁡−1xdx=x22sin⁡−1x−12(12sin⁡−1x−x21−x2)+C\int x \sin^{-1}x dx = \frac{x^2}{2} \sin^{-1}x - \frac{1}{2} \left( \frac{1}{2}\sin^{-1}x - \frac{x}{2}\sqrt{1-x^2} \right) + C =x22sin⁡−1x−14sin⁡−1x+x41−x2+C= \frac{x^2}{2} \sin^{-1}x - \frac{1}{4}\sin^{-1}x + \frac{x}{4}\sqrt{1-x^2} + C Combine the terms with sin⁡−1x\sin^{-1}x: =(x22−14)sin⁡−1x+x41−x2+C= \left( \frac{x^2}{2} - \frac{1}{4} \right) \sin^{-1}x + \frac{x}{4}\sqrt{1-x^2} + C =2x2−14sin⁡−1x+x41−x2+C= \frac{2x^2-1}{4} \sin^{-1}x + \frac{x}{4}\sqrt{1-x^2} + C

The given form of the integral is 2x2−14f(x)+x4g(x)+C\frac{2x^2-1}{4}f(x) + \frac{x}{4}g(x) + C. By comparing our result with the given form, we can identify f(x)f(x) and g(x)g(x): f(x)=sin⁡−1xf(x) = \sin^{-1}x g(x)=1−x2g(x) = \sqrt{1-x^2}