Solveeit Logo
Login

Question

Question: If $\int x \log(1+x^2)dx = \varphi(x) \log(1+x^2) + \Psi(x) + C$, then...

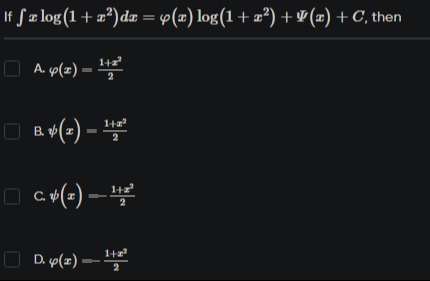
If ∫xlog⁡(1+x2)dx=φ(x)log⁡(1+x2)+Ψ(x)+C\int x \log(1+x^2)dx = \varphi(x) \log(1+x^2) + \Psi(x) + C, then

A

φ(x)=1+x22\varphi(x) = \frac{1+x^2}{2}

B

ψ(x)=1+x22\psi(x) = \frac{1+x^2}{2}

C

ψ(x)=−1+x22\psi(x) = -\frac{1+x^2}{2}

D

φ(x)=−1+x22\varphi(x) = -\frac{1+x^2}{2}

Answer

A, C

Explanation

Solution

We need to evaluate the integral ∫xlog⁡(1+x2)dx\int x \log(1+x^2)dx. Using integration by parts with u=log⁡(1+x2)u = \log(1+x^2) and dv=xdxdv = x dx, we get du=2x1+x2dxdu = \frac{2x}{1+x^2} dx and v=x22v = \frac{x^2}{2}. Applying the integration by parts formula ∫u dv=uv−∫v du\int u \, dv = uv - \int v \, du: ∫xlog⁡(1+x2)dx=x22log⁡(1+x2)−∫x22⋅2x1+x2dx\int x \log(1+x^2)dx = \frac{x^2}{2} \log(1+x^2) - \int \frac{x^2}{2} \cdot \frac{2x}{1+x^2} dx ∫xlog⁡(1+x2)dx=x22log⁡(1+x2)−∫x31+x2dx\int x \log(1+x^2)dx = \frac{x^2}{2} \log(1+x^2) - \int \frac{x^3}{1+x^2} dx To evaluate ∫x31+x2dx\int \frac{x^3}{1+x^2} dx, we can rewrite the integrand as: x31+x2=x(x2+1)−x1+x2=x−x1+x2\frac{x^3}{1+x^2} = \frac{x(x^2+1) - x}{1+x^2} = x - \frac{x}{1+x^2} So, ∫x31+x2dx=∫x dx−∫x1+x2dx=x22−12log⁡(1+x2)\int \frac{x^3}{1+x^2} dx = \int x \, dx - \int \frac{x}{1+x^2} dx = \frac{x^2}{2} - \frac{1}{2} \log(1+x^2) Substituting this back: ∫xlog⁡(1+x2)dx=x22log⁡(1+x2)−(x22−12log⁡(1+x2))+C\int x \log(1+x^2)dx = \frac{x^2}{2} \log(1+x^2) - \left(\frac{x^2}{2} - \frac{1}{2} \log(1+x^2)\right) + C ∫xlog⁡(1+x2)dx=x22log⁡(1+x2)−x22+12log⁡(1+x2)+C\int x \log(1+x^2)dx = \frac{x^2}{2} \log(1+x^2) - \frac{x^2}{2} + \frac{1}{2} \log(1+x^2) + C Grouping terms: ∫xlog⁡(1+x2)dx=(x22+12)log⁡(1+x2)−x22+C\int x \log(1+x^2)dx = \left(\frac{x^2}{2} + \frac{1}{2}\right) \log(1+x^2) - \frac{x^2}{2} + C ∫xlog⁡(1+x2)dx=1+x22log⁡(1+x2)−x22+C\int x \log(1+x^2)dx = \frac{1+x^2}{2} \log(1+x^2) - \frac{x^2}{2} + C Comparing this with the given form φ(x)log⁡(1+x2)+Ψ(x)+C\varphi(x) \log(1+x^2) + \Psi(x) + C, we get φ(x)=1+x22\varphi(x) = \frac{1+x^2}{2} and Ψ(x)=−x22\Psi(x) = -\frac{x^2}{2}. We can rewrite Ψ(x)=−x22\Psi(x) = -\frac{x^2}{2} as Ψ(x)=−1+x2−12=−1+x22+12\Psi(x) = -\frac{1+x^2-1}{2} = -\frac{1+x^2}{2} + \frac{1}{2}. So the integral can be expressed as: ∫xlog⁡(1+x2)dx=1+x22log⁡(1+x2)−1+x22+(C+12)\int x \log(1+x^2)dx = \frac{1+x^2}{2} \log(1+x^2) - \frac{1+x^2}{2} + \left(C + \frac{1}{2}\right) Thus, φ(x)=1+x22\varphi(x) = \frac{1+x^2}{2} (Option A) and Ψ(x)=−1+x22\Psi(x) = -\frac{1+x^2}{2} (Option C) are correct.