Solveeit Logo
Login

Question

Question: If $\int (\sin 2x - \cos 2x) dx = \frac{1}{\sqrt{2}} \sin (2x - a) + C$, then...

If ∫(sin⁡2x−cos⁡2x)dx=12sin⁡(2x−a)+C\int (\sin 2x - \cos 2x) dx = \frac{1}{\sqrt{2}} \sin (2x - a) + C, then

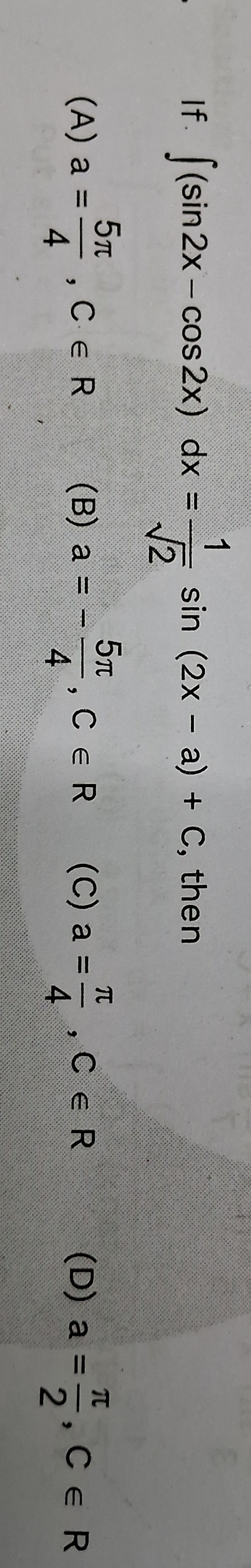
A

a=5π4,CERa = \frac{5\pi}{4}, CER

B

a=−5π4,CERa = -\frac{5\pi}{4}, CER

C

a=π4,CERa = \frac{\pi}{4}, CER

D

a=π2,CERa = \frac{\pi}{2}, CER

Answer

a = -\frac{5\pi}{4}, CER

Explanation

Solution

Here's the step-by-step explanation:

  1. Integrate the left-hand side (LHS):

    ∫(sin⁡2x−cos⁡2x)dx=−12cos⁡2x−12sin⁡2x+C=−12(cos⁡2x+sin⁡2x)+C\int (\sin 2x - \cos 2x) dx = -\frac{1}{2} \cos 2x - \frac{1}{2} \sin 2x + C = -\frac{1}{2} (\cos 2x + \sin 2x) + C

  2. Compare with the right-hand side (RHS):

    −12(cos⁡2x+sin⁡2x)=12sin⁡(2x−a)-\frac{1}{2} (\cos 2x + \sin 2x) = \frac{1}{\sqrt{2}} \sin (2x - a)

  3. Manipulate the equation:

    Multiply both sides by 2\sqrt{2}:

    −22(cos⁡2x+sin⁡2x)=sin⁡(2x−a)-\frac{\sqrt{2}}{2} (\cos 2x + \sin 2x) = \sin (2x - a)

    −12cos⁡2x−12sin⁡2x=sin⁡(2x−a)-\frac{1}{\sqrt{2}} \cos 2x - \frac{1}{\sqrt{2}} \sin 2x = \sin (2x - a)

    Using the trigonometric identity sin⁡(A−B)=sin⁡Acos⁡B−cos⁡Asin⁡B\sin(A-B) = \sin A \cos B - \cos A \sin B:

    sin⁡(2x−a)=sin⁡2xcos⁡a−cos⁡2xsin⁡a\sin (2x - a) = \sin 2x \cos a - \cos 2x \sin a

    Comparing coefficients:

    cos⁡a=−12\cos a = -\frac{1}{\sqrt{2}} and sin⁡a=12\sin a = \frac{1}{\sqrt{2}}

  4. Solve for a:

    The angle 'a' is in the second quadrant. The principal value is a=3π4a = \frac{3\pi}{4}. The general solution is a=3π4+2nπa = \frac{3\pi}{4} + 2n\pi, where nn is an integer.

  5. Check the options:

    For n=−1n = -1, a=3π4−2π=−5π4a = \frac{3\pi}{4} - 2\pi = -\frac{5\pi}{4}.