Question
Question: If $\int \frac{sin^4 x cos^2 x + cos^4 x sin^2 x}{(sin^5 x + cos^3 x sin^2 x + sin^3 x cos^2 x + cos...
If ∫(sin5x+cos3xsin2x+sin3xcos2x+cos5x)2sin4xcos2x+cos4xsin2xdx=α(1+tanβx)−1+C, where α,β∈R then α+β is equal to _______.
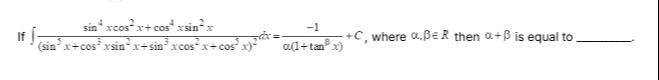
6
Solution
The problem asks us to evaluate a definite integral and then determine the values of α and β by comparing our result with a given form. Finally, we need to find the sum α+β.
Let the given integral be I. I=∫(sin5x+cos3xsin2x+sin3xcos2x+cos5x)2sin4xcos2x+cos4xsin2xdx
Step 1: Simplify the numerator. The numerator (N) is sin4xcos2x+cos4xsin2x. We can factor out sin2xcos2x: N=sin2xcos2x(sin2x+cos2x) Since sin2x+cos2x=1, the numerator simplifies to: N=sin2xcos2x
Step 2: Simplify the term inside the parenthesis in the denominator. Let T=sin5x+cos3xsin2x+sin3xcos2x+cos5x. Group terms: T=(sin5x+sin3xcos2x)+(cos3xsin2x+cos5x) Factor out common terms from each group: T=sin3x(sin2x+cos2x)+cos3x(sin2x+cos2x) Since sin2x+cos2x=1: T=sin3x(1)+cos3x(1) T=sin3x+cos3x So, the denominator (D) is (sin3x+cos3x)2.
Step 3: Rewrite the integral with the simplified numerator and denominator. The integral becomes: I=∫(sin3x+cos3x)2sin2xcos2xdx
Step 4: Transform the integrand for substitution. To make the integral solvable, we can divide both the numerator and the denominator by a suitable power of cosx. Dividing by cos6x (which is (cos3x)2) will convert the expression into terms of tanx and secx.
Numerator transformation: cos6xsin2xcos2x=cos4xsin2x=cos2xsin2x⋅cos2x1=tan2xsec2x
Denominator transformation: cos6x(sin3x+cos3x)2=(cos3xsin3x+cos3x)2=(cos3xsin3x+cos3xcos3x)2=(tan3x+1)2
Now, the integral is: I=∫(tan3x+1)2tan2xsec2xdx
Step 5: Use substitution to evaluate the integral. Let u=tan3x+1. Differentiate u with respect to x: dxdu=dxd(tan3x+1)=3tan2x⋅dxd(tanx)=3tan2xsec2x From this, we get du=3tan2xsec2xdx, or tan2xsec2xdx=31du.
Substitute u and du into the integral: I=∫u21⋅31du I=31∫u−2du
Step 6: Integrate u−2. I=31(−2+1u−2+1)+C I=31(−1u−1)+C I=−3u1+C
Step 7: Substitute back u=tan3x+1. I=−3(tan3x+1)1+C This can be written as: I=−3(1+tan3x)1+C
Step 8: Compare the result with the given form. The given form is α(1+tanβx)−1+C. By comparing our result I=−3(1+tan3x)1+C with the given form, we can identify the values of α and β: α=3 β=3
Step 9: Calculate α+β. α+β=3+3=6
The final answer is 6.
The final answer is 6.
Subject, Chapter, and Topic:
Subject: Mathematics Chapter: Integrals Topic: Integration by Substitution
Difficulty Level:
Medium
Question Type:
Integer
