Question
Question: If $\int \frac{\sec^2xdx}{(\tan^{101}x+\tanx)}=g(x)+c$, where $g(\frac{\pi}{2})=\frac{ln(\frac{1}{2}...
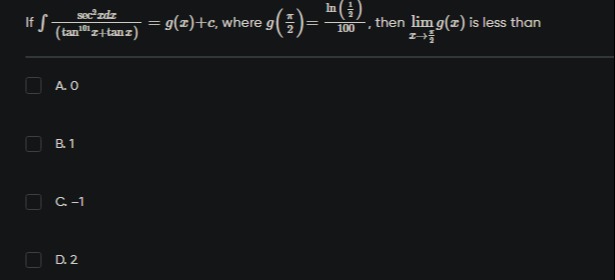
If ∫(tan101x+\tanx)sec2xdx=g(x)+c, where g(2π)=100ln(21), then limx→2πg(x) is less than
0
1
-1
2
The limit is 100−ln(2). Options A, B, and D are all correct as the limit is less than 0, 1, and 2 respectively. Option A provides the tightest upper bound.
Solution
Let u=tanx, so du=sec2xdx. The integral becomes ∫u(u100+u)du=∫u2(u100+1)du. To simplify, we can rewrite the integrand as u2(u100+1)1=u102(1+u−100)1. Alternatively, we can write u(u100+u)1=u101(1+u−100)1. Let's use the substitution v=u100. Then dv=100u99du. The integral is ∫u100(u100+1)u99du=∫v(v+1)1100dv. Using partial fractions, v(v+1)1=v1−v+11. So, the integral is 1001∫(v1−v+11)dv=1001(ln∣v∣−ln∣v+1∣)+c=1001ln∣v+1v∣+c. Substituting back v=tan100x, we get g(x)=1001ln∣tan100x+1tan100x∣+c.
Now, we find the limit as x→2π: As x→2π, tanx→∞. Let u=tanx. limx→2πg(x)=limu→∞(1001lnu100+1u100+c) =1001ln(limu→∞u100+1u100)+c =1001ln(limu→∞1+u10011)+c =1001ln(1)+c=0+c=c.
We are given g(2π)=100ln(21). Assuming g(x) is continuous at 2π, g(2π)=limx→2πg(x). So, c=100ln(21)=100−ln(2).
The limit is 100−ln(2). We need to find which option is greater than this limit. ln(2)≈0.693. So the limit is approximately −0.00693. A. Is −0.00693<0? Yes. B. Is −0.00693<1? Yes. C. Is −0.00693<−1? No. D. Is −0.00693<2? Yes.
The options that the limit is less than are A, B, and D.
