Question

If $\int \frac{dx}{1+x+x^2+x^3}=\frac{1}{a}\tan^{-1}x + \log \sqrt{|b+x|}-\frac{1}{c}\log \sqrt{1+x^d}+C$, where $C$ is a constant of integration, then $a+b+c+d$ is

Answer 1

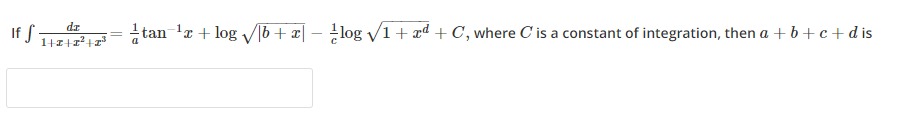
7

Answer 2

To solve the integral $\int \frac{dx}{1+x+x^2+x^3}$, we first factorize the denominator:

$1+x+x^2+x^3 = (1+x) + x^2(1+x) = (1+x)(1+x^2)$.

Now, we decompose the integrand into partial fractions:

$\frac{1}{(1+x)(1+x^2)} = \frac{A}{1+x} + \frac{Bx+C}{1+x^2}$

Multiply both sides by $(1+x)(1+x^2)$:

$1 = A(1+x^2) + (Bx+C)(1+x)$

To find $A$, set $x=-1$:

$1 = A(1+(-1)^2) + (B(-1)+C)(1-1)$

$1 = A(2) + 0 \implies A = \frac{1}{2}$

To find $B$ and $C$, expand the equation and compare coefficients:

$1 = A+Ax^2 + Bx+Bx^2 + C+Cx$

$1 = (A+B)x^2 + (B+C)x + (A+C)$

Comparing coefficients:

Coefficient of $x^2$: $A+B = 0 \implies \frac{1}{2}+B = 0 \implies B = -\frac{1}{2}$

Coefficient of $x$: $B+C = 0 \implies -\frac{1}{2}+C = 0 \implies C = \frac{1}{2}$

Constant term: $A+C = 1 \implies \frac{1}{2}+\frac{1}{2} = 1 \implies 1=1$ (This confirms our values)

So, the partial fraction decomposition is:

$\frac{1}{(1+x)(1+x^2)} = \frac{1/2}{1+x} + \frac{(-1/2)x+1/2}{1+x^2} = \frac{1}{2(1+x)} + \frac{1-x}{2(1+x^2)}$

This can be rewritten as:

$\frac{1}{2(1+x)} + \frac{1}{2(1+x^2)} - \frac{x}{2(1+x^2)}$

Now, we integrate each term:

$\int \frac{dx}{1+x+x^2+x^3} = \int \frac{1}{2(1+x)}dx + \int \frac{1}{2(1+x^2)}dx - \int \frac{x}{2(1+x^2)}dx$

1. $\int \frac{1}{2(1+x)}dx = \frac{1}{2}\log|1+x|$

2. $\int \frac{1}{2(1+x^2)}dx = \frac{1}{2}\tan^{-1}x$

3. For $\int -\frac{x}{2(1+x^2)}dx$, let $u = 1+x^2$. Then $du = 2xdx$, so $xdx = \frac{1}{2}du$.

$\int -\frac{1}{2(1+x^2)} \cdot xdx = \int -\frac{1}{2u} \cdot \frac{1}{2}du = -\frac{1}{4}\int \frac{1}{u}du = -\frac{1}{4}\log|u| = -\frac{1}{4}\log(1+x^2)$ (since $1+x^2 > 0$)

Combining these results, the integral is:

$\frac{1}{2}\log|1+x| + \frac{1}{2}\tan^{-1}x - \frac{1}{4}\log(1+x^2) + C$

Now, we compare this result with the given form:

$\frac{1}{a}\tan^{-1}x + \log \sqrt{|b+x|}-\frac{1}{c}\log \sqrt{1+x^d}+C$

Let's rearrange our result to match the given form:

$\frac{1}{2}\tan^{-1}x + \frac{1}{2}\log|1+x| - \frac{1}{4}\log(1+x^2) + C$

Comparing term by term:

1. For the $\tan^{-1}x$ term:

$\frac{1}{a}\tan^{-1}x = \frac{1}{2}\tan^{-1}x \implies a=2$.

2. For the $\log \sqrt{|b+x|}$ term:

Our term is $\frac{1}{2}\log|1+x|$. Using the property $k\log M = \log M^k$:

$\frac{1}{2}\log|1+x| = \log(|1+x|^{1/2}) = \log \sqrt{|1+x|}$.

Comparing this with $\log \sqrt{|b+x|}$, we get $b=1$.

3. For the $-\frac{1}{c}\log \sqrt{1+x^d}$ term:

Our term is $-\frac{1}{4}\log(1+x^2)$.

Let's rewrite the given form using the property $k\log M = \log M^k$ and $\sqrt{M} = M^{1/2}$:

$-\frac{1}{c}\log \sqrt{1+x^d} = -\frac{1}{c}\log (1+x^d)^{1/2} = -\frac{1}{c} \cdot \frac{1}{2} \log (1+x^d) = -\frac{1}{2c}\log(1+x^d)$.

Now, equate this to our term:

$-\frac{1}{2c}\log(1+x^d) = -\frac{1}{4}\log(1+x^2)$

Comparing the coefficients of $\log$:

$-\frac{1}{2c} = -\frac{1}{4} \implies \frac{1}{2c} = \frac{1}{4} \implies 2c = 4 \implies c=2$.

Comparing the arguments of $\log$:

$1+x^d = 1+x^2 \implies d=2$.

So, we have the values:

$a=2$

$b=1$

$c=2$

$d=2$

Finally, we need to find $a+b+c+d$:

$a+b+c+d = 2+1+2+2 = 7$.