Question
Question: If, $\int \frac{d\theta}{cos^2\theta(tan2\theta+sec2\theta)} = \lambda tan\theta + 2log_e|f(\theta)|...
If, ∫cos2θ(tan2θ+sec2θ)dθ=λtanθ+2loge∣f(θ)∣+c (where c is a constant of integration), then the ordered pair (λ,∣f(θ)∣) is equal to
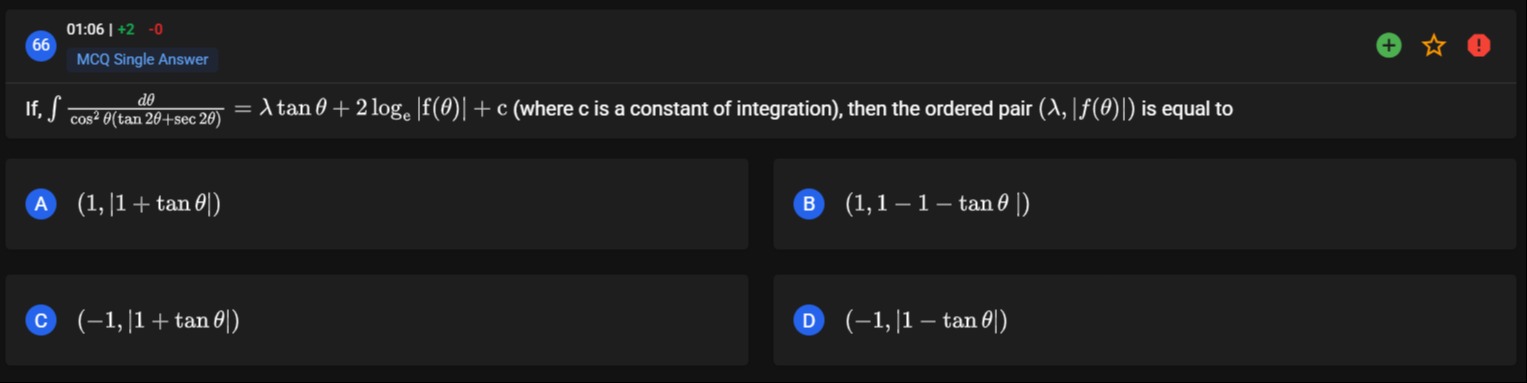
(1, |1 + tan θ|)
(1, |1 - tan θ|)
(-1, |1 + tan θ|)
(-1, |1 - tan θ|)
Option C (-1, |1+tanθ|)
Solution
To solve the given integral, we'll follow these steps:
-
Substitution:
Let u=tanθ. Then, du=sec2θdθ=cos2θdθ.
The integral becomes:∫tan2θ+sec2θdu
-
Express tan2θ and sec2θ in terms of u:
tan2θ=1−tan2θ2tanθ=1−u22u
sec2θ=cos2θ1=1−u21+u2
Then,
tan2θ+sec2θ=1−u22u+1−u21+u2=1−u22u+1+u2
-
Substitute back into the integral:
∫1−u22u+1+u2du=∫u2+2u+11−u2du
Notice that u2+2u+1=(u+1)2 and 1−u2=(1−u)(1+u). Thus,
∫(u+1)2(1−u)(1+u)du=∫u+11−udu
-
Simplify and integrate:
Write:
1+u1−u=1+u2−1
Therefore,
∫1+u1−udu=∫[1+u2−1]du=2∫1+u1du−∫1du
∫1+u1−udu=2ln∣1+u∣−u+C
-
Substitute back u=tanθ:
−tanθ+2ln∣1+tanθ∣+C
Comparing with the given form λtanθ+2ln∣f(θ)∣+C, we find:
λ=−1,f(θ)=1+tanθ
Thus, the ordered pair (λ,∣f(θ)∣) is (−1,∣1+tanθ∣).
