Question

If $\int \frac{\cos 2x \sin 4x}{\cos^4 x(1+\cos^2 2x)}dx = 2\log_e (1 + \cos 2x)-\log_e (1 + \cos^2 2x) + f(x) + c$, where $c$ is a constant of integration, then $f(x)$ is

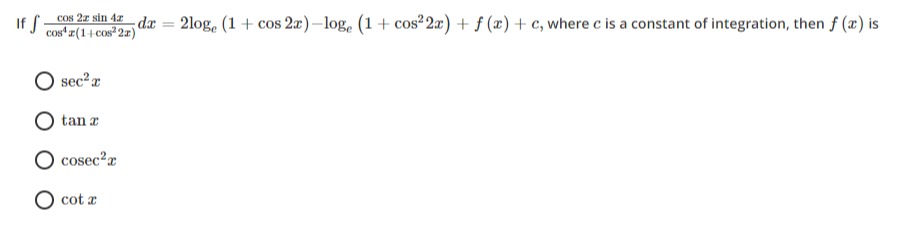
• A. sec$^2x$
• B. tan $x$
• C. cosec$^2x$
• D. cot $x$

Answer 1

Answer: (A)

sec$^2x$

Answer 2

To solve this problem, we need to find the function $f(x)$ given the integral expression. The key steps involve simplifying the integrand, using trigonometric identities, applying substitution, and decomposing the rational function into partial fractions.

1. Simplify the Integrand:

   • Use the identity $\sin 4x = 2 \sin 2x \cos 2x$.
   • Use the identity $\cos^2 x = \frac{1+\cos 2x}{2}$, which implies $\cos^4 x = \frac{(1+\cos 2x)^2}{4}$.
   • Substitute these into the integrand to get: $$\frac{8 \sin 2x \cos^2 2x}{(1+\cos 2x)^2(1+\cos^2 2x)}$$

2. Apply Substitution:

   • Let $u = \cos 2x$, so $du = -2 \sin 2x dx$. This transforms the integral.

3. Partial Fraction Decomposition:

   • Decompose the rational function $\frac{u^2}{(1+u)^2(1+u^2)}$ into partial fractions: $$\frac{u^2}{(1+u)^2(1+u^2)} = \frac{A}{1+u} + \frac{B}{(1+u)^2} + \frac{Cu+D}{1+u^2}$$
   • Solve for the constants $A, B, C, D$.

4. Integration:

   • Integrate each term of the partial fraction decomposition with respect to $u$.

5. Substitute Back:

   • Substitute back $u = \cos 2x$ to express the result in terms of $x$.

6. Identify f(x):

   • Compare the obtained result with the given form $2\log_e (1 + \cos 2x)-\log_e (1 + \cos^2 2x) + f(x) + c$ to identify $f(x)$.
   • Simplify $f(x)$ using the identity $1+\cos 2x = 2\cos^2 x$.

Following these steps, we find that $f(x) = \sec^2 x$.