Question
Question: If $\int \frac{4e^x+6e^{-x}}{9e^x-4e^{-x}}dx=Ax+Blog(9e^{2x}-4)+C$, then $A=..., B=...$ and $C=......
If ∫9ex−4e−x4ex+6e−xdx=Ax+Blog(9e2x−4)+C, then A=...,B=... and $C=...
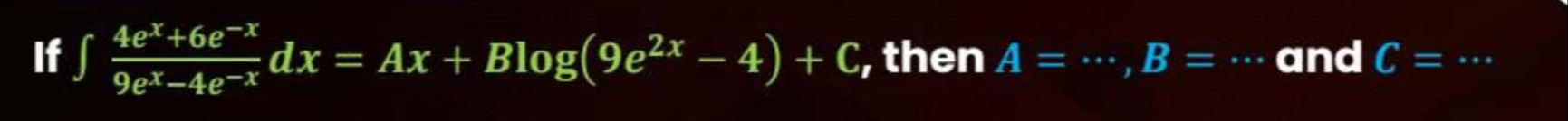
A = -3/2, B = 35/36; C = const. of integration
A = 3/2, B = -35/36; C = const. of integration
A = -19/36, B = 35/36; C = const. of integration
A = 19/36, B = -35/36; C = const. of integration
A = -3/2, B = 35/36; C = const. of integration
Solution
Let I=∫9ex−4e−x4ex+6e−xdx. We express the numerator as a linear combination of the denominator and its derivative. Let D(x)=9ex−4e−x. Then D′(x)=9ex+4e−x. We set 4ex+6e−x=λ(9ex−4e−x)+μ(9ex+4e−x). Comparing coefficients of ex and e−x: 9λ+9μ=4 −4λ+4μ=6 Solving these equations gives λ=−3619 and μ=3635. The integral becomes: I=∫(λ+μD(x)D′(x))dx=λx+μln∣D(x)∣+C I=−3619x+3635ln∣9ex−4e−x∣+C. Using ln∣9ex−4e−x∣=ln∣e−x(9e2x−4)∣=−x+ln∣9e2x−4∣: I=−3619x+3635(−x+ln∣9e2x−4∣)+C I=(−3619−3635)x+3635ln∣9e2x−4∣+C I=−3654x+3635ln∣9e2x−4∣+C I=−23x+3635ln∣9e2x−4∣+C. Comparing with Ax+Blog(9e2x−4)+C, we get A=−23 and B=3635.
