Question

If $\int \frac{3x^2+2}{\sqrt{x^2-x+1}}dx = ax\sqrt{x^2-x+1}+\frac{9}{4}\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C,$ where $C$ is constant of integration, then the value of $a+4b$ is

Answer 1

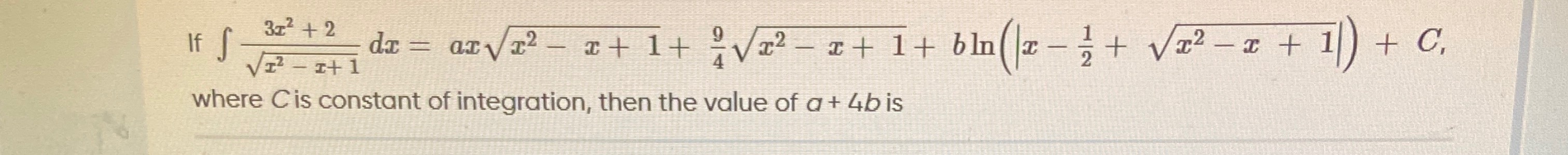
8

Answer 2

The problem asks us to find the value of $a+4b$ given an integral equation. The given integral is $\int \frac{3x^2+2}{\sqrt{x^2-x+1}}dx$. The form of the result is $ax\sqrt{x^2-x+1}+\frac{9}{4}\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C$. This can be written as $(ax+\frac{9}{4})\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C$.

Let $I = \int \frac{3x^2+2}{\sqrt{x^2-x+1}}dx$. We can use the general method for integrals of the form $\int \frac{P(x)}{\sqrt{Q(x)}} dx$, where $P(x)$ and $Q(x)$ are quadratic polynomials. We express $P(x)$ in terms of $Q(x)$, $Q'(x)$ and a constant: $P(x) = \lambda Q(x) + \mu Q'(x) + \nu$ Here, $P(x) = 3x^2+2$ and $Q(x) = x^2-x+1$. $Q'(x) = 2x-1$. So, we write $3x^2+2 = \lambda(x^2-x+1) + \mu(2x-1) + \nu$. Expanding the right side: $3x^2+2 = \lambda x^2 - \lambda x + \lambda + 2\mu x - \mu + \nu$ $3x^2+2 = \lambda x^2 + (-\lambda+2\mu)x + (\lambda-\mu+\nu)$

Comparing the coefficients of powers of $x$:

1. Coefficient of $x^2$: $\lambda = 3$.
2. Coefficient of $x$: $-\lambda+2\mu = 0$. Substitute $\lambda=3$: $-3+2\mu = 0 \implies 2\mu = 3 \implies \mu = \frac{3}{2}$.
3. Constant term: $\lambda-\mu+\nu = 2$. Substitute $\lambda=3$ and $\mu=\frac{3}{2}$: $3-\frac{3}{2}+\nu = 2$. $\frac{6-3}{2}+\nu = 2 \implies \frac{3}{2}+\nu = 2 \implies \nu = 2-\frac{3}{2} = \frac{1}{2}$.

Now substitute this expression for $3x^2+2$ back into the integral: $I = \int \frac{3(x^2-x+1) + \frac{3}{2}(2x-1) + \frac{1}{2}}{\sqrt{x^2-x+1}} dx$ $I = \int \left[ 3\frac{x^2-x+1}{\sqrt{x^2-x+1}} + \frac{3}{2}\frac{2x-1}{\sqrt{x^2-x+1}} + \frac{1}{2}\frac{1}{\sqrt{x^2-x+1}} \right] dx$ $I = 3\int \sqrt{x^2-x+1} dx + \frac{3}{2}\int \frac{2x-1}{\sqrt{x^2-x+1}} dx + \frac{1}{2}\int \frac{1}{\sqrt{x^2-x+1}} dx$

Let's evaluate each part:

1. $\int \frac{2x-1}{\sqrt{x^2-x+1}} dx$: Let $u = x^2-x+1$, then $du = (2x-1)dx$. $\int \frac{du}{\sqrt{u}} = \int u^{-1/2} du = \frac{u^{1/2}}{1/2} = 2\sqrt{u} = 2\sqrt{x^2-x+1}$. So, $\frac{3}{2}\int \frac{2x-1}{\sqrt{x^2-x+1}} dx = \frac{3}{2} (2\sqrt{x^2-x+1}) = 3\sqrt{x^2-x+1}$.

2. $\int \frac{1}{\sqrt{x^2-x+1}} dx$: Complete the square in the denominator: $x^2-x+1 = (x-\frac{1}{2})^2 - (\frac{1}{2})^2 + 1 = (x-\frac{1}{2})^2 + \frac{3}{4}$. This is of the form $\int \frac{1}{\sqrt{y^2+k^2}} dy = \ln|y+\sqrt{y^2+k^2}|$. Here $y=x-\frac{1}{2}$ and $k=\frac{\sqrt{3}}{2}$. So, $\int \frac{1}{\sqrt{x^2-x+1}} dx = \ln|x-\frac{1}{2}+\sqrt{(x-\frac{1}{2})^2+\frac{3}{4}}| = \ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$. Thus, $\frac{1}{2}\int \frac{1}{\sqrt{x^2-x+1}} dx = \frac{1}{2}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$.

3. $\int \sqrt{x^2-x+1} dx$: This is of the form $\int \sqrt{y^2+k^2} dy = \frac{y}{2}\sqrt{y^2+k^2} + \frac{k^2}{2}\ln|y+\sqrt{y^2+k^2}|$. Here $y=x-\frac{1}{2}$ and $k^2=\frac{3}{4}$. $\int \sqrt{x^2-x+1} dx = \frac{x-\frac{1}{2}}{2}\sqrt{x^2-x+1} + \frac{3/4}{2}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$ $= (\frac{x}{2}-\frac{1}{4})\sqrt{x^2-x+1} + \frac{3}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$. So, $3\int \sqrt{x^2-x+1} dx = 3\left[ (\frac{x}{2}-\frac{1}{4})\sqrt{x^2-x+1} + \frac{3}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| \right]$ $= (\frac{3x}{2}-\frac{3}{4})\sqrt{x^2-x+1} + \frac{9}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$.

Combining all parts: $I = (\frac{3x}{2}-\frac{3}{4})\sqrt{x^2-x+1} + \frac{9}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| + 3\sqrt{x^2-x+1} + \frac{1}{2}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| + C$ Group terms with $\sqrt{x^2-x+1}$: $(\frac{3x}{2}-\frac{3}{4}+3)\sqrt{x^2-x+1} = (\frac{3x}{2}+\frac{-3+12}{4})\sqrt{x^2-x+1} = (\frac{3x}{2}+\frac{9}{4})\sqrt{x^2-x+1}$. Group terms with $\ln$: $(\frac{9}{8}+\frac{1}{2})\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| = (\frac{9+4}{8})\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| = \frac{13}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$.

So, $I = (\frac{3x}{2}+\frac{9}{4})\sqrt{x^2-x+1} + \frac{13}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| + C$.

Comparing this with the given form: $ax\sqrt{x^2-x+1}+\frac{9}{4}\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C$ $= (ax+\frac{9}{4})\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C$.

By comparison: $a = \frac{3}{2}$ $b = \frac{13}{8}$

We need to find the value of $a+4b$. $a+4b = \frac{3}{2} + 4(\frac{13}{8})$ $a+4b = \frac{3}{2} + \frac{13}{2}$ $a+4b = \frac{3+13}{2} = \frac{16}{2} = 8$.

The final answer is $\boxed{8}$.

Explanation:

The given integral is of the form $\int \frac{P(x)}{\sqrt{Q(x)}} dx$, where $P(x)=3x^2+2$ and $Q(x)=x^2-x+1$. We express $P(x)$ as $\lambda Q(x) + \mu Q'(x) + \nu$. By comparing coefficients, we found $\lambda=3$, $\mu=\frac{3}{2}$, and $\nu=\frac{1}{2}$. This transforms the integral into three parts:

1. $3\int \sqrt{x^2-x+1} dx$
2. $\frac{3}{2}\int \frac{2x-1}{\sqrt{x^2-x+1}} dx$
3. $\frac{1}{2}\int \frac{1}{\sqrt{x^2-x+1}} dx$

Each part is integrated using standard formulas.

• The second integral simplifies to $3\sqrt{x^2-x+1}$.
• The third integral simplifies to $\frac{1}{2}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|$.
• The first integral requires completing the square for $x^2-x+1$ to $(x-\frac{1}{2})^2+\frac{3}{4}$, then using $\int \sqrt{y^2+k^2} dy = \frac{y}{2}\sqrt{y^2+k^2} + \frac{k^2}{2}\ln|y+\sqrt{y^2+k^2}|$. This yields $3\left[ (\frac{x}{2}-\frac{1}{4})\sqrt{x^2-x+1} + \frac{3}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}| \right]$.

Combining all terms and simplifying, the integral result is $(\frac{3x}{2}+\frac{9}{4})\sqrt{x^2-x+1} + \frac{13}{8}\ln|x-\frac{1}{2}+\sqrt{x^2-x+1}|+C$. Comparing this with the given form $(ax+\frac{9}{4})\sqrt{x^2-x+1}+b\ln(|x-\frac{1}{2}+\sqrt{x^2-x+1}|)+C$, we identify $a=\frac{3}{2}$ and $b=\frac{13}{8}$. Finally, $a+4b = \frac{3}{2} + 4(\frac{13}{8}) = \frac{3}{2} + \frac{13}{2} = \frac{16}{2} = 8$.

The final answer is $\boxed{8}$.