Solveeit Logo
Login

Question

Question: If $\int \frac{2x-\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx = C-2\sqrt{1-x^2}-\frac{2}{3}\sqrt{f(x)}$ then ...

If ∫2x−sin⁡−1x1−x2dx=C−21−x2−23f(x)\int \frac{2x-\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx = C-2\sqrt{1-x^2}-\frac{2}{3}\sqrt{f(x)} then f(x)f(x) is equal to

A

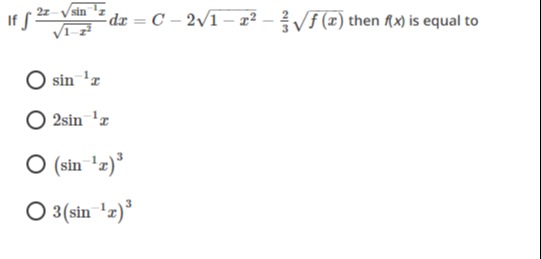
sin⁡−1x\sin^{-1}x

B

(sin⁡−1x)3/2(\sin^{-1}x)^{3/2}

C

(sin⁡−1x)3(\sin^{-1}x)^3

D

(sin⁡−1x)2/3(\sin^{-1}x)^{2/3}

Answer

(sin⁡−1x)3(\sin^{-1}x)^3

Explanation

Solution

The given integral is ∫2x−sin⁡−1x1−x2dx\int \frac{2x-\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx. We split the integral into two parts:

I=∫2x1−x2dx−∫sin⁡−1x1−x2dxI = \int \frac{2x}{\sqrt{1-x^2}}dx - \int \frac{\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx

Let's evaluate the first part, I1=∫2x1−x2dxI_1 = \int \frac{2x}{\sqrt{1-x^2}}dx. Let u=1−x2u = 1-x^2. Then du=−2x dxdu = -2x \, dx, so 2x dx=−du2x \, dx = -du. Substitute these into the integral I1I_1:

I1=∫−duu=−∫u−1/2du=−u1/21/2+C1=−2u+C1=−21−x2+C1I_1 = \int \frac{-du}{\sqrt{u}} = -\int u^{-1/2} du = -\frac{u^{1/2}}{1/2} + C_1 = -2\sqrt{u} + C_1 = -2\sqrt{1-x^2} + C_1

Next, let's evaluate the second part, I2=−∫sin⁡−1x1−x2dxI_2 = -\int \frac{\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx. Let t=sin⁡−1xt = \sin^{-1}x. Then dt=11−x2dxdt = \frac{1}{\sqrt{1-x^2}}dx. Substitute these into the integral I2I_2:

I2=−∫t dt=−∫t1/2dt=−t3/23/2+C2=−23t3/2+C2=−23(sin⁡−1x)3/2+C2I_2 = -\int \sqrt{t} \, dt = -\int t^{1/2} dt = -\frac{t^{3/2}}{3/2} + C_2 = -\frac{2}{3}t^{3/2} + C_2 = -\frac{2}{3}(\sin^{-1}x)^{3/2} + C_2

Combining I1I_1 and I2I_2, the complete integral is:

∫2x−sin⁡−1x1−x2dx=I1+I2=−21−x2−23(sin⁡−1x)3/2+(C1+C2)\int \frac{2x-\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx = I_1 + I_2 = -2\sqrt{1-x^2} - \frac{2}{3}(\sin^{-1}x)^{3/2} + (C_1+C_2)

Let C=C1+C2C = C_1+C_2 be the arbitrary constant of integration. So, we have:

∫2x−sin⁡−1x1−x2dx=C−21−x2−23(sin⁡−1x)3/2\int \frac{2x-\sqrt{\sin^{-1}x}}{\sqrt{1-x^2}}dx = C - 2\sqrt{1-x^2} - \frac{2}{3}(\sin^{-1}x)^{3/2}

The problem states that the integral is equal to C−21−x2−23f(x)C-2\sqrt{1-x^2}-\frac{2}{3}\sqrt{f(x)}. Comparing our result with the given form:

C−21−x2−23(sin⁡−1x)3/2=C−21−x2−23f(x)C - 2\sqrt{1-x^2} - \frac{2}{3}(\sin^{-1}x)^{3/2} = C - 2\sqrt{1-x^2} - \frac{2}{3}\sqrt{f(x)}

By comparing the terms, we can see that:

−23(sin⁡−1x)3/2=−23f(x)-\frac{2}{3}(\sin^{-1}x)^{3/2} = -\frac{2}{3}\sqrt{f(x)}

Multiply both sides by −32-\frac{3}{2}:

(sin⁡−1x)3/2=f(x)(\sin^{-1}x)^{3/2} = \sqrt{f(x)}

To find f(x)f(x), square both sides of the equation:

f(x)=((sin⁡−1x)3/2)2=(sin⁡−1x)3f(x) = \left((\sin^{-1}x)^{3/2}\right)^2 = (\sin^{-1}x)^3