Question
Question: If $\int \frac{1}{x^4+8x^2+9}dx = \frac{1}{k}\left[ \frac{1}{\sqrt{14}}\tan^{-1}(f(x)) - \frac{1}{\s...
If ∫x4+8x2+91dx=k1[141tan−1(f(x))−21tan−1(g(x))]+c,
then 2k+f(3)+g(1)=
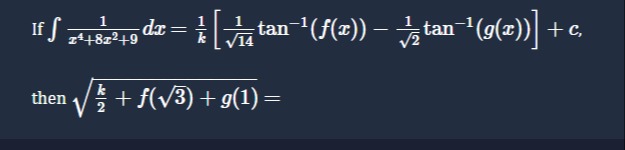
2+1
Solution
The integral we need to solve is I=∫x4+8x2+91dx. This is a standard type of integral involving x4. We can divide the numerator and denominator by x2. I=∫x2+8+9/x21/x2dx.
We can rewrite the denominator using the identity x2+x2a2=(x±xa)2∓2a. Here, a=3. So, x2+x29=(x−x3)2+6 or x2+x29=(x+x3)2−6. The denominator is x2+9/x2+8. Using the first identity: x2+9/x2+8=(x−3/x)2+6+8=(x−3/x)2+14. Using the second identity: x2+9/x2+8=(x+3/x)2−6+8=(x+3/x)2+2.
The numerator is 1/x2. The derivative of (x−3/x) is 1+3/x2, and the derivative of (x+3/x) is 1−3/x2. We can express 1/x2 as a linear combination of these derivatives: x21=A(1+x23)+B(1−x23) x21=(A+B)+x23(A−B). Comparing coefficients of 1 and 1/x2: A+B=0 3(A−B)=1⟹A−B=1/3. Adding the two equations: 2A=1/3⟹A=1/6. Subtracting the second from the first: 2B=−1/3⟹B=−1/6. So, x21=61(1+x23)−61(1−x23).
Substitute this back into the integral: I=∫x2+9/x2+861(1+x23)−61(1−x23)dx I=61∫(x−3/x)2+141+3/x2dx−61∫(x+3/x)2+21−3/x2dx.
For the first integral, let u=x−3/x. Then du=(1+3/x2)dx. The integral becomes ∫u2+(14)2du. ∫u2+(14)2du=141tan−1(14u)=141tan−1(14x−3/x)=141tan−1(x14x2−3).
For the second integral, let v=x+3/x. Then dv=(1−3/x2)dx. The integral becomes ∫v2+(2)2dv. ∫v2+(2)2dv=21tan−1(2v)=21tan−1(2x+3/x)=21tan−1(x2x2+3).
Combining the results, we get: I=61[141tan−1(x14x2−3)−21tan−1(x2x2+3)]+c.
The given form is k1[141tan−1(f(x))−21tan−1(g(x))]+c. Comparing the two forms, we identify: k=6. f(x)=x14x2−3. g(x)=x2x2+3.
We need to evaluate the expression 2k+f(3)+g(1). First, calculate the required values: k=6. f(3)=314(3)2−3=423−3=420=0. g(1)=12(1)2+3=21+3=24=242=22.
Now substitute these values into the expression: 2k+f(3)+g(1)=26+0+22=3+22.
To simplify 3+22, we look for two numbers whose sum is 3 and product is 2. These numbers are 2 and 1. So, 3+22=(2)2+(1)2+2⋅2⋅1=(2+1)2. 3+22=(2+1)2=∣2+1∣. Since 2+1 is positive, ∣2+1∣=2+1.
The value of the expression is 2+1.
