Question
Question: If $\int \frac{(1+e^x).e^x}{(1+e^x)^2+1}dx = ln(\sqrt{g(x)})+C$, and $g(1)=(1+e)^2+1$ then the value...
If ∫(1+ex)2+1(1+ex).exdx=ln(g(x))+C, and g(1)=(1+e)2+1 then the value of g(0) is equal to
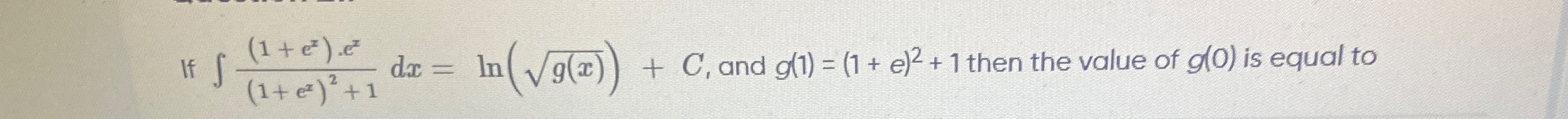
5
Solution
To solve the given problem, we need to evaluate the integral and then use the given conditions to find the value of g(0).
Step 1: Evaluate the integral The given integral is ∫(1+ex)2+1(1+ex).exdx. Let's use the substitution method. Let t=1+ex. Differentiating both sides with respect to x, we get: dt=exdx.
Now, substitute t and dt into the integral: ∫t2+1tdt This integral is of the form ∫f(x)f′(x)dx=ln∣f(x)∣+C, if we consider f(t)=t2+1. The derivative of t2+1 is 2t. So, we need to adjust the numerator by a factor of 2. ∫t2+1tdt=21∫t2+12tdt Now, apply the integration formula: 21ln∣t2+1∣+C Substitute back t=1+ex: 21ln((1+ex)2+1)+C Since (1+ex)2+1 is always positive for all real x, we can remove the absolute value signs: 21ln((1+ex)2+1)+C
Step 2: Match the result with the given form We are given that the integral is equal to ln(g(x))+C. Let's rewrite our result using logarithm properties (alnb=lnba): 21ln((1+ex)2+1)=ln(((1+ex)2+1)1/2)=ln((1+ex)2+1) Comparing this with ln(g(x))+C, we can identify g(x): g(x)=(1+ex)2+1
Step 3: Verify the given condition The problem states that g(1)=(1+e)2+1. Let's check our derived g(x) for x=1: g(1)=(1+e1)2+1=(1+e)2+1 This matches the given condition, confirming our expression for g(x) is correct.
Step 4: Calculate the value of g(0) Substitute x=0 into the expression for g(x): g(0)=(1+e0)2+1 Since e0=1: g(0)=(1+1)2+1 g(0)=(2)2+1 g(0)=4+1 g(0)=5
The final answer is 5.
Explanation of the solution: The integral ∫(1+ex)2+1(1+ex).exdx is solved by substituting t=1+ex, which leads to dt=exdx. The integral transforms to ∫t2+1tdt. This is equal to 21ln(t2+1)+C. Substituting back t=1+ex, we get 21ln((1+ex)2+1)+C. Using logarithm properties, this becomes ln((1+ex)2+1)+C. Comparing this with the given ln(g(x))+C, we find g(x)=(1+ex)2+1. Finally, evaluate g(0)=(1+e0)2+1=(1+1)2+1=22+1=5.
