Question
Question: If $\int e^x (x^3 + x^2 - x + 4) dx = e^x f(x) + c$, then $f(1) =$...
If ∫ex(x3+x2−x+4)dx=exf(x)+c, then f(1)=
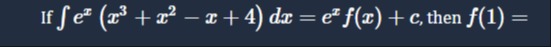
3
Solution
The given integral is ∫ex(x3+x2−x+4)dx. We are given that the integral is equal to exf(x)+c. This integral is of the form ∫exP(x)dx, where P(x) is a polynomial. A standard result for such integrals is ∫exP(x)dx=ex(P(x)−P′(x)+P′′(x)−P′′′(x)+…)+c, where the derivatives are taken until they become zero.
In this case, P(x)=x3+x2−x+4. Let's find the derivatives of P(x):
P′(x)=dxd(x3+x2−x+4)=3x2+2x−1
P′′(x)=dxd(3x2+2x−1)=6x+2
P′′′(x)=dxd(6x+2)=6
P(4)(x)=dxd(6)=0
Using the formula, the integral is:
∫ex(x3+x2−x+4)dx=ex(P(x)−P′(x)+P′′(x)−P′′′(x))+c
=ex((x3+x2−x+4)−(3x2+2x−1)+(6x+2)−(6))+c
=ex(x3+x2−x+4−3x2−2x+1+6x+2−6)+c
Combine the terms inside the parenthesis:
=ex(x3+(1−3)x2+(−1−2+6)x+(4+1+2−6))+c
=ex(x3−2x2+3x+1)+c
We are given that ∫ex(x3+x2−x+4)dx=exf(x)+c. Comparing this with our result, we find that f(x)=x3−2x2+3x+1.
We need to find the value of f(1). Substitute x=1 into the expression for f(x):
f(1)=(1)3−2(1)2+3(1)+1
f(1)=1−2(1)+3(1)+1
f(1)=1−2+3+1
f(1)=5−2
f(1)=3
