Question

If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio (or proportion). Then prove that the two triangles are similar.

Answer 1

Hint:In this question first we will use the cosine formula on the equal angle and show that if their corresponding sides are in the same ratio then the third side will also be in the same ratio and with all that it will be proved that the two triangles are similar.

Complete step-by-step answer:

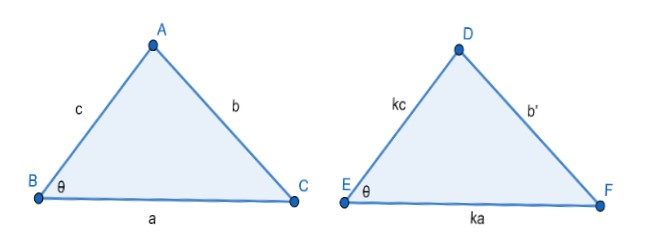
Let’s look at this figure.
As per the question $\angle ABC=\angle DEF$ and if AB = c then DE = kc and if BC = a then EF = ka.
Similarity of two triangles: Two triangles, $~~\Delta ABC$ and $\Delta DEF$, are similar if and only if corresponding angles have the same measure: this implies that they are similar if and only if the lengths of corresponding sides are proportional.
Here k is the ratio as mentioned in the question.
The cosine formula is: $\cos \theta =\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}$ …………….. (1)
Now using this formula in $\Delta DEF$ we get $\cos \theta =\dfrac{{{(ka)}^{2}}+{{(kc)}^{2}}-b{{'}^{2}}}{2{{k}^{2}}ac}$ ……………… (2)
Equating (1) and (2) we get,
$\begin{aligned} & \dfrac{{{(ka)}^{2}}+{{(kc)}^{2}}-b{{'}^{2}}}{2{{k}^{2}}ac}=\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac} \\\ & \Rightarrow {{\text{k}}^{2}}{{a}^{2}}+{{k}^{2}}{{c}^{2}}-b{{'}^{2}}={{\text{k}}^{2}}{{a}^{2}}+{{k}^{2}}{{c}^{2}}-{{k}^{2}}{{b}^{2}} \\\ & \Rightarrow b'=kb \\\ \end{aligned}$
(Cancelling 2ac from both sides and then taking ${{k}^{2}}$ on the opposite side)
Hence, all the three sides have the same ratio ‘k’.
From this we can conclude that and are similar to each other.

Note: We can also solve this question by using some property of similarity, like AAA. As we have shown all the sides are in the same ratio after that we have to use cosine formula for the other two angles and we have to show that all three corresponding angles are the same for the two triangles and hence by AAA these two triangles will be similar.
.