Question

If in the system of capillary tube, the mass of the liquid climbing in the tube is M. Find out the mass of the tube in case the radius of the tube is doubled?

Answer 1

We are given that the radius of a capillary tube is increased twice. The mass of the liquid in the capillary column seems to be related to the radius. We can substitute the relations between the parameters involved in capillary rise to find this.

Complete step by step answer:
We know that the capillary rise of a liquid in a capillary tube is related to the radius of the tube and the density of the liquid. The density of the liquid can be used to find the relation between the mass of the liquid in the column to the height of the column.
We know that the Pressure involved in rising the liquid column to a height ‘h’, which acts against the atmospheric pressure is given by –
$P=h\rho g$
Where $\rho$is the density of the liquid in the capillary tube.
We can derive the equation for the height of the capillary rise from the surface tension relations as –
$h=\dfrac{2S\cos \theta }{r\rho g}$

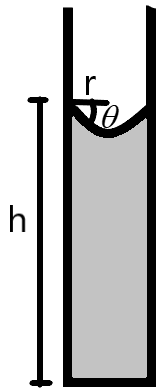
Where, S is the surface tension of the liquid.
$\theta$ is the angle of contact of the liquid with the tube.
r is the radius of the tube.
Now, we know the mass and the density are related each other to as –

& m=\rho hA \\\ & \\\ \end{aligned}$$ Where, A is the area of the top circular face of the tube. We can substitute the quantities for each of the parameter to get the relation between the mass and the radius as – $$\begin{aligned} & \Rightarrow m=\rho \dfrac{2S\cos \theta }{r\rho g}\pi {{r}^{2}} \\\ & \therefore m=\dfrac{2S\pi r\cos \theta }{g} \\\ & \Rightarrow \text{ }m\propto r \\\ \end{aligned}$$ From this we understand that the mass of the liquid in the capillary tube is directly proportional to the radius of the tube. Therefore, when the radius of the tube is doubled, the mass in the column also doubles. So, if the mass of the liquid initially was ‘m’, then the final mass when the radius is doubled becomes ‘2m’. **Note:** We should substitute all the quantities involved in height calculation with the basic parameters to get the correct result. If we let the area be ‘A’ itself, there is a probability that we will not consider the square factor of radius in the term and will get an absolutely different answer.