Question
Question: If in the below diagram after opening the valve, final pressure is \[\dfrac{7}{6}MPa\], then find th...
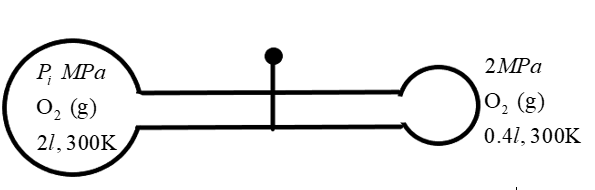
If in the below diagram after opening the valve, final pressure is 67MPa, then find the initial pressure P1 (in MPa).
Solution
We are given two containers connected by a pipe which has unequal pressure and volume conditions initially. The thermodynamic variables are kept steady by separating them with a valve, which is opened later. We can use the gas law to solve the unknown variable.
Complete step by step answer:
We are given a condition in which unequal states of thermodynamic conditions mix with each other resulting in another state. Two bulb-like containers of volume V1 and V2 contains gaseous oxygen at pressure P1 and P2respectively at a temperature 300K. We know that the gaseous oxygen tends to have a different number of molecules at different thermodynamic conditions. So, initially the number of molecules in the containers are given as n1 and n2 respectively.

Now, let us consider the situation when the valve is opened. We know for sure that the oxygen molecules tend to move across the pipe due to the pressure difference at the two ends. So, what we have to calculate is the resulting conditions which will be observed as a result of this opening.
For this, we can apply the gas law. The gas law is given as –
PV=nRT
Where, P is the pressure in the container,
V is the volume of the container,
n is the number of molecules in the container,
R is the gas constant, and,
T is the temperature in absolute scale.
Let us consider this gas law equation for the two containers in the initial condition.
For first container,
