Question

If in a triangle ABC, $\dfrac{2\operatorname{cosA}}{a}+\dfrac{\operatorname{cosB}}{b}+\dfrac{2\operatorname{cosC}}{c}=\dfrac{a}{bc}+\dfrac{b}{ac}$, find the $\angle A$=

& \left( a \right){{90}^{\circ }} \\\ & \left( b \right){{60}^{\circ }} \\\ & \left( c \right){{30}^{\circ }} \\\ & \left( d \right)\text{none of these} \\\ \end{aligned}$$

Answer 1

Hint: This question can be solved by applying the cosine rule in a triangle and then substituting the corresponding cosine formula in the given equation and then again try to write the solved equation in terms of cosine to get the angle.
$\operatorname{cosA}=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$

Complete step-by-step answer:

Let us look at the formula of cosine rule in a triangle ABC:

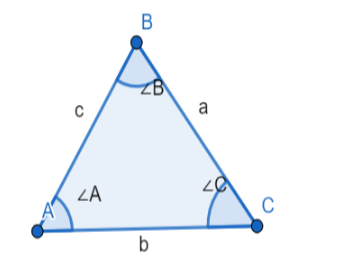
In a triangle ABC, the angles are denoted by capital letters A, B, C and the lengths of the sides opposite to these angles are denoted by small letters a, b, c respectively.
Now, the formula of cosine rule is:

& \operatorname{cosA}=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc},............\left( 1 \right) \\\ & \operatorname{cosB}=\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac},.................\left( 2 \right) \\\ & \operatorname{cosC}=\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab},...............\left( 3 \right)\text{ } \\\ \end{aligned}$$ From, the equation given in the question we get, $$\Rightarrow \dfrac{2\operatorname{cosA}}{a}+\dfrac{\operatorname{cosB}}{b}+\dfrac{2\operatorname{cosC}}{c}=\dfrac{a}{bc}+\dfrac{b}{ac}$$ By substituting the above cosine formulae from the equations (1), (2), (3) in the above equation we get, $$\Rightarrow \dfrac{2\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc} \right)}{a}+\dfrac{\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}}{b}+\dfrac{2\left( \dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{2ab} \right)}{c}=\dfrac{a}{bc}+\dfrac{b}{ac}$$ Now, by multiplying the 2 inside the bracket we can write it as: $$\Rightarrow \dfrac{\left( \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{bc} \right)}{a}+\dfrac{\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2ac}}{b}+\dfrac{\left( \dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{ab} \right)}{c}=\dfrac{a}{bc}+\dfrac{b}{ac}$$ Then, by writing the denominators in each term together we get, $$\Rightarrow \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{abc}+\dfrac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2abc}+\dfrac{{{a}^{2}}+{{b}^{2}}-{{c}^{2}}}{abc}=\dfrac{a}{bc}+\dfrac{b}{ac}$$ Now, by taking the LCM on the left hand side and taking the term 2abc common we can write it as: $$\Rightarrow \dfrac{1}{2abc}\left[ 2\left( {{b}^{2}}+{{c}^{2}}-{{a}^{2}} \right)+\left( {{a}^{2}}+{{c}^{2}}-{{b}^{2}} \right)+2\left( {{a}^{2}}+{{b}^{2}}-{{c}^{2}} \right) \right]=\dfrac{a}{bc}+\dfrac{b}{ac}$$ Then, by multiplying the 2 inside the bracket and then writing them on the left side and on the right hand side by LCM and then taking the abc term common outside we get, $$\Rightarrow \dfrac{1}{2abc}\left[ 2{{b}^{2}}+2{{c}^{2}}-2{{a}^{2}}+{{a}^{2}}+{{c}^{2}}-{{b}^{2}}+2{{a}^{2}}+2{{b}^{2}}-2{{c}^{2}} \right]=\dfrac{1}{abc}\left( {{a}^{2}}+{{b}^{2}} \right)$$ Now, by cancelling the abc term on both sides and solving the addition terms we get, $$\Rightarrow \dfrac{1}{2}\left[ 3{{b}^{2}}+{{c}^{2}}+{{a}^{2}} \right]={{a}^{2}}+{{b}^{2}}$$ Now, take the 2 on the left hand side and multiply it on the right hand side. $$\Rightarrow 3{{b}^{2}}+{{c}^{2}}+{{a}^{2}}=2{{a}^{2}}+2{{b}^{2}}$$ Here, bring all the terms to the same side and simplify it then we get, $$\Rightarrow {{b}^{2}}+{{c}^{2}}-{{a}^{2}}=0$$ Now, by dividing with 2bc on both sides we get, $$\Rightarrow \dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}=0$$ As we already know that from the cosine formula that: $$\operatorname{cosA}=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$$ By considering this we get, $$\begin{aligned} & \Rightarrow \operatorname{cosA}=0 \\\ & \therefore \angle A={{90}^{\circ }} \\\ \end{aligned}$$ $$\left[ \because \cos {{90}^{\circ }}=0 \right]$$ Hence, the correct option is (a). Note: Using the cosine formula is the crucial step here and while substituting it in the given equation we need to cross check about 2 and multiply it accordingly wherever it is given. There are possibilities for minor calculations error in addition and subtraction where care should be taken while writing the equations. While cancelling the abc term on both sides we need to be careful about the 2 in the denominator on the left hand side. At the concluding step writing the equation obtained in terms of the sides of the triangle in the form of cosine gives us the required result. $$\operatorname{cosA}=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc}$$.