Question

If in a triangle ABC, B is the orthocentre and if circumcentre of triangle ABC is ( 2,4) and vertex A is ( 0,0) then coordinate of vertex C is
(a) $\left( 4,2 \right)$
(b) $\left( 4,8 \right)$
(c) $\left( 8,4 \right)$
(d) $\left( 8,2 \right)$

Answer 1

Hint: A right angled triangle can always be inscribed inside a circle with the hypotenuse as the diameter of the circle and the midpoint of the hypotenuse of the triangle will be the circumcentre of the triangle .

Consider the figure alongside . In the question it is given that $B$ is the orthocentre. We also know that $B$ is one of the vertices of the triangle $ABC$.

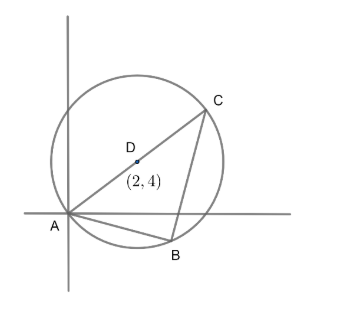
So , we can conclude that $ABC$ is a right-angled triangle.
Now , we know that a right angled triangle can be inscribed in a circle with the hypotenuse as the diameter.
So , we can conclude that $AC$ is the diameter of a circle.
So , the centre of this circle will be the midpoint of the diameter.
Now, we know the midpoint of line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)...............\left( i \right)$
Now , we will consider $\left( x,y \right)$ to be the coordinates of $C$.
We know , circumcentre of a triangle is the centre of the circle circumscribing the triangle.
So , the circumcentre $D\left( 2,4 \right)$ is the midpoint of the line joining $A\left( 0,0 \right)$ and $C\left( x,y \right)$.
Now , we will use the equation $\left( i \right)$ to find the coordinates of the vertex $C$.
So , from equation$\left( i \right)$ , we have
$2=\dfrac{x+0}{2}\Rightarrow x=4$
And $\text{ 4}=\dfrac{y+0}{2}\Rightarrow y=8$
So , the coordinates of vertex $C$ are $\left( 4,8 \right)$.
Option B - $\left( 4,8 \right)$ is correct answer

Note: The midpoint of line joining the points $\left( {{x}_{1}},{{y}_{1}} \right)\text{ and }\left( {{x}_{2}},{{y}_{2}} \right)$ is given as:
$\left( \dfrac{\left( {{x}_{1}}+{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}+{{y}_{2}} \right)}{2} \right)$ and not $\left( \dfrac{\left( {{x}_{1}}-{{x}_{2}} \right)}{2},\dfrac{\left( {{y}_{1}}-{{y}_{2}} \right)}{2} \right)$ . Students often get confused between the two. Due to this confusion , they generally end up getting a wrong answer . So , such mistakes should be avoided .