Question

If in a parallelogram ABCD, the coordinate of A, B and C are respectively $\left( 1,2 \right)$, $\left( 3,4 \right)$ and $\left( 2,5 \right)$ , Find the equation of the diagonal BD is:
(a) $5x+3y-11=0$
(b) $x-3y+9=0$
(c) $3x+5y-13=0$
(d) $5x-3y+9=0$

Answer 1

Hint : We have points $A\left( 1,2 \right)$ , $B\left( 3,4 \right)$ and $C\left( 2,5 \right)$ given so, we use the fact that diagonals AC and BD intersects at their midpoint. We find the midpoint of the diagonal AC using the midpoint formula. Since diagonal passes through this midpoint and point B, we find the equation of diagonal BD.

Complete step-by-step answer :
Given that we have a parallelogram ABCD, which has vertices $A\left( 1,2 \right)$ , $B\left( 3,4 \right)$ and $C\left( 2,5 \right)$ .
We need to find the equation of the diagonal BD.
We draw the given information into the figure no to get a better view.

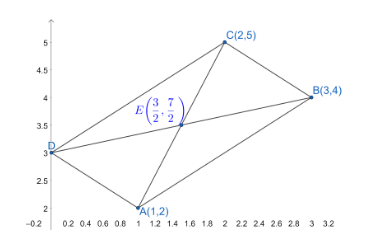
We know that to find the equation we at least need two points if no slope is given. We have one point $B\left( 3,4 \right)$ given and we need one more point to find the equation of diagonal BD.
We know that diagonals of a parallelogram AC and BD intersects at their midpoint. So, to find the equation of the diagonal BD, we need to find the midpoint of diagonal AC.
We know that the midpoint of two points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( \dfrac{{{x}_{1}}+{{x}_{2}}}{2},\dfrac{{{y}_{1}}+{{y}_{2}}}{2} \right)$ .
We have points $A\left( 1,2 \right)$ and $C\left( 2,5 \right)$ of diagonal AC and we need to find the midpoint of diagonal AC. Let the midpoint be E.
$E=\left( \dfrac{1+2}{2},\dfrac{2+5}{2} \right)$ .
$E=\left( \dfrac{3}{2},\dfrac{7}{2} \right)$ .
Now, we have point E and from the figure we can observe that the diagonal BD passes through point B and point E.
We know that the equation of a straight line passing through points $\left( {{x}_{1}},{{y}_{1}} \right)$ and $\left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( y-{{y}_{1}} \right)=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\times \left( x-{{x}_{1}} \right)$ .
We have points $B\left( 3,4 \right)$ and $E=\left( \dfrac{3}{2},\dfrac{7}{2} \right)$ to find the equation of BD.
The equation of straight-line BD is $y-4=\left( \dfrac{\dfrac{7}{2}-4}{\dfrac{3}{2}-3} \right)\times \left( x-3 \right)$ .
$y-4=\left( \dfrac{\dfrac{7-8}{2}}{\dfrac{3-6}{2}} \right)\times \left( x-3 \right)$ .
$y-4=\left( \dfrac{-1}{-3} \right)\times \left( x-3 \right)$ .
$y-4=\left( \dfrac{1}{3} \right)\times \left( x-3 \right)$ .
$3\times \left( y-4 \right)=1\times \left( x-3 \right)$ .
$3y-12=x-3$ .
$x-3y-3+12=0$ .
$x-3y+9=0$ .
∴ The equation of the diagonal is $x-3y+9=0$ .
So, the correct answer is “Option B”.

Note : We make mistakes by substituting the coordinates of point either ‘B’ or ‘E’ in options and conclude the answer which should be avoided. As diagonal passes through both ‘B’ and ‘E’, we need to check with the both points to solve alternatively. Here, we found an equation of diagonal ‘BD’ ; sometimes we can be asked to find an equation of diagonal ‘AD’.