Solveeit Logo
Login

Question

Question: If in a \(\Delta ABC\) ,a = 6 , b = 3 and cos ( A – B ) = \(\dfrac{4}{5}\) then find its area ?...

If in a ΔABC\Delta ABC ,a = 6 , b = 3 and cos ( A – B ) = 45\dfrac{4}{5} then find its area ?

Explanation

Solution

With the given details we can apply it in the formula tan⁡(A−B2)=1−cos⁡(A−B)1+cos⁡(A−B)\tan \left( {\dfrac{{A - B}}{2}} \right) = \sqrt {\dfrac{{1 - \cos \left( {A - B} \right)}}{{1 + \cos \left( {A - B} \right)}}} and we know that tan⁡(A−B2)=a−ba+bcot⁡C2\tan \left( {\dfrac{{A - B}}{2}} \right) = \dfrac{{a - b}}{{a + b}}\cot \dfrac{C}{2}using which we can find the value of C and since its 90 degree we can find the area using the formula 12∗base∗height\dfrac{1}{2}*base*height.

Complete step-by-step answer:
We are given that a = 6 cm and b = 3 cm and cos ( A – B ) = 45\dfrac{4}{5}
We know that tan⁡(A−B2)=1−cos⁡(A−B)1+cos⁡(A−B)\tan \left( {\dfrac{{A - B}}{2}} \right) = \sqrt {\dfrac{{1 - \cos \left( {A - B} \right)}}{{1 + \cos \left( {A - B} \right)}}}
Now applying the given value we get,
⇒tan⁡(A−B2)=1−451+45 ⇒tan⁡(A−B2)=5−455+45 ⇒tan⁡(A−B2)=19=13  \Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right) = \sqrt {\dfrac{{1 - \dfrac{4}{5}}}{{1 + \dfrac{4}{5}}}} \\\ \Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right) = \sqrt {\dfrac{{\dfrac{{5 - 4}}{5}}}{{\dfrac{{5 + 4}}{5}}}} \\\ \Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right) = \sqrt {\dfrac{1}{9}} = \dfrac{1}{3} \\\
Using this we can substitute in the formula
⇒tan⁡(A−B2)=a−ba+bcot⁡C2\Rightarrow \tan \left( {\dfrac{{A - B}}{2}} \right) = \dfrac{{a - b}}{{a + b}}\cot \dfrac{C}{2}
Substituting all the known values,
⇒13=6−36+3cot⁡C2 ⇒13=39cot⁡C2 ⇒13=13cot⁡C2 ⇒cot⁡C2=1 ⇒C2=cot⁡−1(1)=π4 ⇒C=2π4=π2  \Rightarrow \dfrac{1}{3} = \dfrac{{6 - 3}}{{6 + 3}}\cot \dfrac{C}{2} \\\ \Rightarrow \dfrac{1}{3} = \dfrac{3}{9}\cot \dfrac{C}{2} \\\ \Rightarrow \dfrac{1}{3} = \dfrac{1}{3}\cot \dfrac{C}{2} \\\ \Rightarrow \cot \dfrac{C}{2} = 1 \\\ \Rightarrow \dfrac{C}{2} = {\cot ^{ - 1}}(1) = \dfrac{\pi }{4} \\\ \Rightarrow C = \dfrac{{2\pi }}{4} = \dfrac{\pi }{2} \\\
From this we get that the angle C is a right angle
Therefore the triangle ABC is a right angle triangle , right angled at B

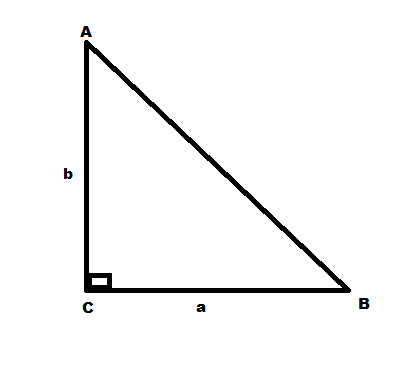
Therefore the area of the triangle = 12∗base∗height\dfrac{1}{2}*base*height sq . units
=12∗a∗b\dfrac{1}{2}*a*b
=12∗6∗3=12∗18=9sq.units\dfrac{1}{2}*6*3 = \dfrac{1}{2}*18 = 9sq.units
Therefore the area of the triangle is 9 sq.units

Note: Here we get to know that it’s a right triangle hence we use the side AC as its height but if it is not an right triangle the altitude may vary.