Question

If in a ∆ABC, $\angle A = 3\angle B$, then prove that $\sin B = \dfrac{1}{2}\sqrt {\dfrac{{3b - a}}{b}}$

Answer 1

Hint : Here a, b and c are the lengths of sides and $\angle A,\angle B,\angle C$ are the angles of the given triangle ABC. We can use sine law to prove that $\sin B = \dfrac{1}{2}\sqrt {\dfrac{{3b - a}}{b}}$ which is mentioned below and substitute the value of $\sin A$ in terms of angle B. Use appropriate formulas from below and solve the question.
Formulas used:
1. According to the law of sines, $\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}$, where a, b and c are the lengths of sides and $\angle A,\angle B,\angle C$ are the angles of a triangle ABC.
2. $\sin 3A = 3\sin A - 4{\sin ^3}A$

Complete step-by-step answer :
We are given that in a triangle ABC $\angle A = 3\angle B$. We have to prove that $\sin B = \dfrac{1}{2}\sqrt {\dfrac{{3b - a}}{b}}$.
A triangle has three sides, three vertices and three angles.
Here in triangle ABC, a, b and c are the lengths of its sides and $\angle A,\angle B,\angle C$ are its angles.
The side opposite to angle A is a, opposite to angle B is b and opposite to angle C is c.

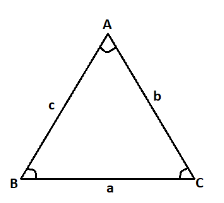
So according to the sine rule or law of sines or sine law or sine formula, $\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}$
Here we need to prove the value of $\sin B$ and we are given the relation between angle A and angle B.
So we are considering the first two terms of $\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b} = \dfrac{{\sin C}}{c}$.
$\dfrac{{\sin A}}{a} = \dfrac{{\sin B}}{b}$
Substitute the value of angle A in terms of angle B.
$\Rightarrow \dfrac{{\sin 3B}}{a} = \dfrac{{\sin B}}{b}$
$\Rightarrow a \times \sin B = b \times \sin 3B$
Sending ‘a’ from LHS to RHS
$\Rightarrow \sin B = \dfrac{{b\sin 3B}}{a} = \dfrac{b}{a}\sin 3B$
Replace $\sin 3B$ with its formula, $\sin 3A = 3\sin A - 4{\sin ^3}A$ here in the place of A we are putting B.
$\Rightarrow \sin B = \dfrac{b}{a}\left( {3\sin B - 4{{\sin }^3}B} \right)$
Putting all the terms left side, we get
$\Rightarrow \sin B - \dfrac{b}{a}\left( {3\sin B - 4{{\sin }^3}B} \right) = 0$
Taking out $\sin B$ common, we get
$\Rightarrow \sin B\left[ {1 - \dfrac{b}{a}\left( {3 - 4{{\sin }^2}B} \right)} \right] = 0$
As we can see the LHS of the above equation is a multiplication of $\sin B$ and $\left[ {1 - \dfrac{b}{a}\left( {3 - 4{{\sin }^2}B} \right)} \right]$
Considering $\sin B$ as x and $\left[ {1 - \dfrac{b}{a}\left( {3 - 4{{\sin }^2}B} \right)} \right]$ as y, we get $xy = 0$
So either x must be zero or y must be zero or both can be zero for the equation to become zero.
But angle B cannot be zero; this means $\sin B$ (x) cannot be zero. So here y should be zero.
Therefore, $1 - \dfrac{b}{a}\left( {3 - 4{{\sin }^2}B} \right) = 0$
$\Rightarrow \dfrac{b}{a}\left( {3 - 4{{\sin }^2}B} \right) = 1$
$\Rightarrow 3 - 4{\sin ^2}B = \dfrac{a}{b}$
$\Rightarrow 4{\sin ^2}B = 3 - \dfrac{a}{b}$
$\Rightarrow 4{\sin ^2}B = \dfrac{{3b - a}}{b}$
$\Rightarrow {\sin ^2}B = \dfrac{1}{4}\left( {\dfrac{{3b - a}}{b}} \right)$
$\Rightarrow \sin B = \sqrt {\dfrac{1}{4}\left( {\dfrac{{3b - a}}{b}} \right)} = \dfrac{1}{2}\sqrt {\left( {\dfrac{{3b - a}}{b}} \right)}$
Therefore, $\sin B = \dfrac{1}{2}\sqrt {\left( {\dfrac{{3b - a}}{b}} \right)}$
Hence, proved.

Note : Always do not confuse in considering ‘a’ as the side opposite to angle A but not its adjacent side. And law of sines can also be used to find the unknown sides of a triangle when two angles and one side are given. This rule is mostly used in scalene triangles (triangles with three different sides).