Solveeit Logo
Login

Question

Question: If \(\tan \alpha , \tan \beta , \tan \gamma\) are the roots of the equation <img src="https://cdn.p...

If tan⁡α,tan⁡β,tan⁡γ\tan \alpha , \tan \beta , \tan \gamma are the roots of the equation

then the value of

(1 + tanα) (1 + tan2β) (1 + tan2γ) is equal to

A
B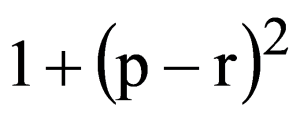
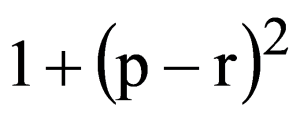
C
D

None of these

Answer
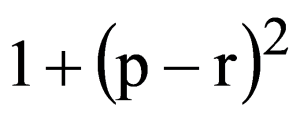
Explanation

Solution

From the given equation we have ∑tan⁡α=p\sum \tan \alpha = p

∑tan⁡αtan⁡β=0\sum \tan \alpha \tan \beta = 0 and tan⁡αtan⁡βtan⁡γ=r\tan \alpha \tan \beta \tan \gamma = \mathrm { r }

so that (1+tan⁡2α)(1+tan⁡2β)(1+tan⁡2γ)\left( 1 + \tan ^ { 2 } \alpha \right) \left( 1 + \tan ^ { 2 } \beta \right) \left( 1 + \tan ^ { 2 } \gamma \right)

=1+∑tan⁡2α+∑tan⁡2αtan⁡2β+tan⁡2αtan⁡2βtan⁡2γ1 + \sum \tan ^ { 2 } \alpha + \sum \tan ^ { 2 } \alpha \tan ^ { 2 } \beta + \tan ^ { 2 } \alpha \tan ^ { 2 } \beta \tan ^ { 2 } \gamma

=1+(∑tan⁡α)2−2∑tan⁡αtan⁡β+(∑tan⁡αtan⁡β)2\left( \sum \tan \alpha \right) ^ { 2 } - 2 \sum \tan \alpha \tan \beta + \left( \sum \tan \alpha \tan \beta \right) ^ { 2 } −2tan⁡αtan⁡βtan⁡β∑tan⁡α+tan⁡2αtan⁡2βtan⁡2γ- 2 \tan \alpha \tan \beta \tan \beta \sum \tan \alpha + \tan ^ { 2 } \alpha \tan ^ { 2 } \beta \tan ^ { 2 } \gamma = 1 + p2−2pr+r2\mathrm { p } ^ { 2 } - 2 \mathrm { pr } + \mathrm { r } ^ { 2 }

=