Question

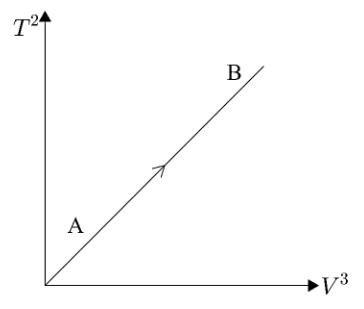
If ideal diatomic gas follows the process, as shown in graph, where $T$ is temperature in kelvin $(K)$ and $V$ is volume $(m^3)$ , then molar heat capacity for this process will be [in terms of gas constant $R$ ]

A. $\dfrac{7R}{2}$
B. $5R\;$
C. $\dfrac{19R}{6}$
D. $\dfrac{11R}{2}$

Answer 1

To find the molar heat capacity, first we need to find the equation of the process from the graph. From the equation of the process we can find the polytropic index. Based on the polytropic index, we can use the predefined equations to find the molar heat capacity using the specific heat at constant volume, specific heat at constant pressure and the universal gas constant.

Formula Used:
General equation of a process,
$P{{V}^{k}}=constant$
where, $P$ is the pressure, $V$ is the volume and $k$ is the polytropic index.
Molar heat Capacity at constant volume,
${{C}_{v}}=\dfrac{f}{2}R$
where, $C_v$ is the specific heat at constant volume, $f$ is the degree of freedom, $R$ is the Universal gas constant.
Molar heat capacity,
$C={{C}_{v}}+\dfrac{R}{1-k}$
where, $C_v$ is the specific heat at constant volume, $R$ is the universal gas constant, $k$ is the polytropic index.

Complete step by step answer:
Here, we are given a graph of ${{T}^{2}}\to {{V}^{3}}$ and the graph shows a straight line passing through the origin. But we know that the equation of a straight line passing through origin can be written as $y=mx$. Here, we are given $T^2$ on the $y-axis$ and $V^3$ on the $x-axis$. Hence, substituting these values in the equation of the straight line we get,
${{T}^{2}}=m{{V}^{3}}$
Multiplying by ${{V}^{-3}}$ on both sides,
${{T}^{2}}{{V}^{-3}}=m$
Applying square root on both the sides,
$\Rightarrow T{{V}^{\dfrac{-3}{2}}}={{m}^{\dfrac{1}{2}}}$
Now, we know that the slope of a straight line is constant and thus, its square root value will also be constant.
$\Rightarrow T{{V}^{\dfrac{-3}{2}}}=constant$ …… $(1)$

Now, we know the ideal gas equation $PV=nRT$ where, $P$ is the pressure, $V$ is the volume, $n$ is the moles of the gas, $R$ is the universal gas constant, $T$ is the temperature.
$\Rightarrow T=\dfrac{PV}{nR}$
Substituting the above equation in equation $(1)$
$\Rightarrow\dfrac{PV}{nR}\cdot {{V}^{\dfrac{-3}{2}}}=constant$
$\Rightarrow P{{V}^{\dfrac{-1}{2}}}=nR\times constant$
For a particular experiment, the number of moles of gas is constant. Hence, all the terms on the right side of the above equation are constant.
$\Rightarrow P{{V}^{\dfrac{-1}{2}}}=constant$ …… $(2)$

Now, let us compare the above equation with the general equation for a thermodynamic process $P{{V}^{k}}=constant$
From the comparison, we obtain the polytropic index $k=\dfrac{-1}{2}$
Now, here we are given that the gas is diatomic and hence, the degrees of freedom for the gas will be $f=5$
From the degrees of freedom, we can find the specific heat at constant volume using the formula ${{C}_{v}}=\dfrac{f}{2}R$
$\Rightarrow{{C}_{v}}=\dfrac{5}{2}R$ …… $(3)$

Now, we can find the molar heat capacity for a polytropic process using the formula
$C={{C}_{v}}+\dfrac{R}{1-k}$
Substituting the values obtained from the above equations,
$C=\dfrac{5}{2}R+\dfrac{R}{1-\left( \dfrac{-1}{2} \right)}$
$\Rightarrow C=\dfrac{5}{2}R+\dfrac{2R}{3}$
Taking the L.C.M. as $6$ ,
$C=\dfrac{15R}{6}+\dfrac{4R}{6}$
$\therefore C=\dfrac{19R}{6}$

Hence, the correct answer is option C.

Note: Here, to find the polytropic index, we have converted the equation in terms of pressure and volume for simplification. We can directly find the polytropic index from the equation of temperature and volume using the equation $T{{V}^{k-1}}=constant$. Also as the process is polytropic, we have used the mentioned formula for molar heat capacity. If the process was adiabatic, isochoric, isobaric or isothermal, we can use the general formula ${{C}_{p}}-{{C}_{v}}=R$ where $C_p$ is the heat capacity at constant pressure, $C_v$ is the heat capacity at constant volume and $R$ is the Universal gas constant.