Question

If $I_n = \int_0^{\pi/4} \tan^n \theta d\theta$, then $I_8 + I_6$ equals

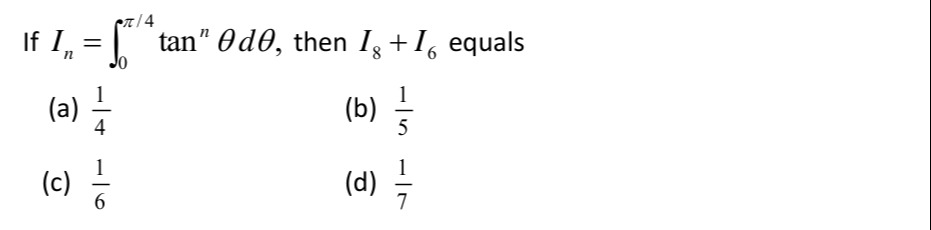
• A. $\frac{1}{4}$
• B. $\frac{1}{5}$
• C. $\frac{1}{6}$
• D. $\frac{1}{7}$

Answer 1

Answer: (D)

$\frac{1}{7}$

Answer 2

Let the given integral be $I_n = \int_0^{\pi/4} \tan^n \theta d\theta$. We want to find the value of $I_8 + I_6$.

Consider the sum $I_n + I_{n-2}$ for $n \ge 2$:

$I_n + I_{n-2} = \int_0^{\pi/4} \tan^n \theta d\theta + \int_0^{\pi/4} \tan^{n-2} \theta d\theta$

$I_n + I_{n-2} = \int_0^{\pi/4} (\tan^n \theta + \tan^{n-2} \theta) d\theta$

$I_n + I_{n-2} = \int_0^{\pi/4} \tan^{n-2} \theta (\tan^2 \theta + 1) d\theta$

Using the identity $\tan^2 \theta + 1 = \sec^2 \theta$, we get:

$I_n + I_{n-2} = \int_0^{\pi/4} \tan^{n-2} \theta \sec^2 \theta d\theta$

Let $u = \tan \theta$. Then $du = \sec^2 \theta d\theta$. When $\theta = 0$, $u = \tan 0 = 0$. When $\theta = \pi/4$, $u = \tan (\pi/4) = 1$.

The integral becomes:

$I_n + I_{n-2} = \int_0^1 u^{n-2} du = \left[ \frac{u^{n-1}}{n-1} \right]_0^1 = \frac{1}{n-1}$ for $n \ge 2$.

We need to find $I_8 + I_6$. This fits the form $I_n + I_{n-2}$ with $n=8$.

Using the reduction formula with $n=8$:

$I_8 + I_{8-2} = I_8 + I_6 = \frac{1}{8-1} = \frac{1}{7}$.

Thus, $I_8 + I_6 = \frac{1}{7}$.