Question
Question: If $I_n = \int_{0}^{\pi} e^x (\sin x)^n dx$, then $5\frac{I_3}{I_1}$, is equal to __________....
If In=∫0πex(sinx)ndx, then 5I1I3, is equal to __________.
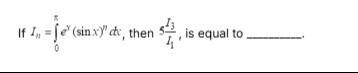
3
Solution
To solve this problem, we need to evaluate the given definite integral In=∫0πex(sinx)ndx and then find the value of 5I1I3.
First, let's derive a reduction formula for In. We will use integration by parts twice. Let In=∫0πex(sinx)ndx. Apply integration by parts with u=(sinx)n and dv=exdx. Then du=n(sinx)n−1(cosx)dx and v=ex.
In=[ex(sinx)n]0π−∫0πexn(sinx)n−1(cosx)dx
Evaluate the boundary term: At x=π: eπ(sinπ)n=eπ(0)n=0 (for n≥1). At x=0: e0(sin0)n=1⋅(0)n=0 (for n≥1). So, the boundary term [ex(sinx)n]0π=0.
Therefore, In=−n∫0πex(sinx)n−1(cosx)dx. (Equation 1)
Now, let's apply integration by parts again to the integral J=∫0πex(sinx)n−1(cosx)dx. Let u′=(sinx)n−1cosx and dv′=exdx. Then v′=ex. To find du′, we differentiate u′ using the product rule: du′=[(n−1)(sinx)n−2(cosx)(cosx)+(sinx)n−1(−sinx)]dx du′=[(n−1)(sinx)n−2cos2x−(sinx)n]dx Substitute cos2x=1−sin2x: du′=[(n−1)(sinx)n−2(1−sin2x)−(sinx)n]dx du′=[(n−1)(sinx)n−2−(n−1)(sinx)n−(sinx)n]dx du′=[(n−1)(sinx)n−2−n(sinx)n]dx.
Now apply integration by parts to J: J=[ex(sinx)n−1cosx]0π−∫0πex[(n−1)(sinx)n−2−n(sinx)n]dx.
Evaluate the boundary term [ex(sinx)n−1cosx]0π: At x=π: eπ(sinπ)n−1cosπ=eπ(0)n−1(−1)=0 (for n−1≥1, i.e., n≥2). At x=0: e0(sin0)n−1cos0=1⋅(0)n−1⋅1=0 (for n−1≥1, i.e., n≥2). So, for n≥2, the boundary term is 0.
Thus, for n≥2: J=−∫0πex[(n−1)(sinx)n−2−n(sinx)n]dx J=−(n−1)∫0πex(sinx)n−2dx+n∫0πex(sinx)ndx Recognize In−2 and In: J=−(n−1)In−2+nIn.
Substitute this expression for J back into Equation 1: In=−n[−(n−1)In−2+nIn] In=n(n−1)In−2−n2In.
Now, rearrange the terms to solve for In: In+n2In=n(n−1)In−2 (1+n2)In=n(n−1)In−2 In=1+n2n(n−1)In−2.
This is the reduction formula for In. We need to find 5I1I3. Using the reduction formula for n=3: I3=1+323(3−1)I3−2 I3=1+93×2I1 I3=106I1 I3=53I1.
Now, we can find the ratio I1I3: I1I3=53.
Finally, calculate 5I1I3: 5I1I3=5×53=3.
Note: We could also calculate I1 explicitly, though it's not required for this specific problem. I1=∫0πexsinxdx. Using the standard integral formula ∫eaxsin(bx)dx=a2+b2eax(asin(bx)−bcos(bx)), with a=1,b=1: I1=[12+12ex(1⋅sinx−1⋅cosx)]0π I1=[2ex(sinx−cosx)]0π I1=2eπ(sinπ−cosπ)−2e0(sin0−cos0) I1=2eπ(0−(−1))−21(0−1) I1=2eπ(1)−21(−1) I1=2eπ+21=2eπ+1.
The final answer is 3.
Explanation of the solution:
- Define In=∫0πex(sinx)ndx.
- Apply integration by parts twice to In to derive a recurrence relation.
- First integration by parts: In=[ex(sinx)n]0π−n∫0πex(sinx)n−1cosxdx. The boundary term is zero.
- Let J=∫0πex(sinx)n−1cosxdx. Apply integration by parts to J: J=[ex(sinx)n−1cosx]0π−∫0πex[(n−1)(sinx)n−2−n(sinx)n]dx. The boundary term is zero for n≥2.
- Substitute J back into the expression for In: In=−n[−(n−1)In−2+nIn].
- Simplify the recurrence relation: (1+n2)In=n(n−1)In−2, which gives In=1+n2n(n−1)In−2.
- Use the recurrence relation for n=3: I3=1+323(3−1)I1=106I1=53I1.
- Calculate the required expression: 5I1I3=5×I153I1=5×53=3.
