Question

If I is the incentre of the triangle ABC; ${{P}_{1}}$, ${{P}_{2}}$ and ${{P}_{3}}$ are the radii of the circumcircle of the triangles IBC, ICA and IAB respectively, then
(a) $2{{P}_{1}}=a\sec \left( \dfrac{A}{2} \right)$
(b) $2{{P}_{2}}=b\sec \left( \dfrac{B}{2} \right)$
(c) $2{{P}_{3}}=c\sec \left( \dfrac{C}{2} \right)$
(d) ${{P}_{1}}{{P}_{2}}{{P}_{3}}=2{{R}^{2}}r$

Answer 1

We start solving the problem by drawing the figure to represent the given information. We then recall the facts that the Incentre is formed by the intersection of angular bisectors in a circle and the sum of angles in the triangle is $\pi$ to get the angles at the incentre. We then make use of the fact that the circumradius of triangle PQR is defined as $\dfrac{p}{2\sin P}=\dfrac{q}{2\sin Q}=\dfrac{r}{2\sin R}$ to get the relations between the circumradius and sides of the triangle. We then multiple the obtain values of ${{P}_{1}}$, ${{P}_{2}}$, ${{P}_{3}}$ and then make use of the results $\sin \alpha =2\sin \left( \dfrac{\alpha }{2} \right)\cos \left( \dfrac{\alpha }{2} \right)$, $r=4R\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{B}{2} \right)\sin \left( \dfrac{C}{2} \right)$ to get the required answer.

Complete step by step answer:
According to the problem, we are given that I is the incentre of the triangle ABC and ${{P}_{1}}$, ${{P}_{2}}$ and ${{P}_{3}}$ are the radii of the circumcircle of the triangles IBC, ICA and IAB respectively. We need to find which of the given options are true.
Let us draw the figure representing the given information.

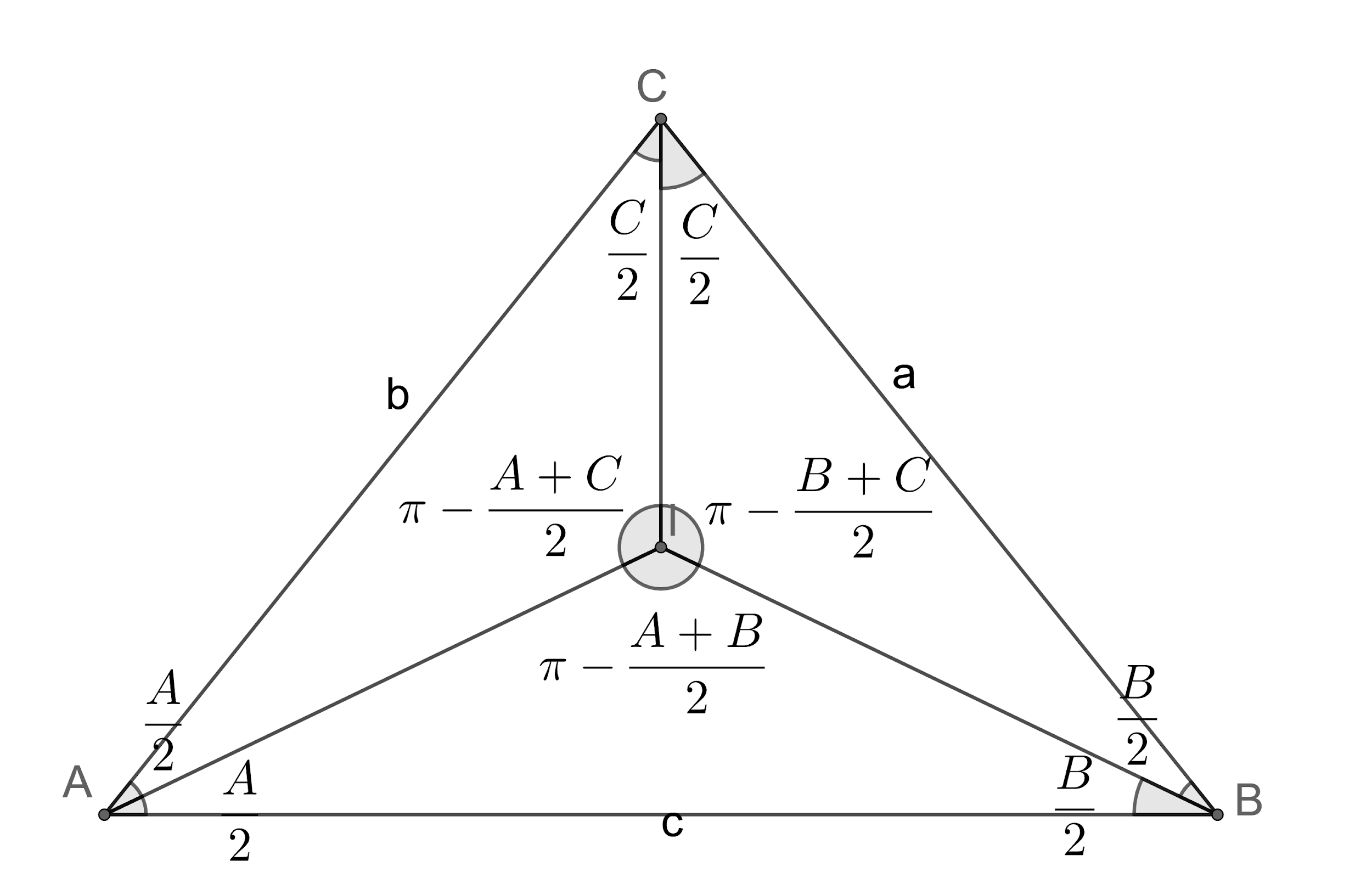
We know that the Incentre is formed by the intersection of angular bisectors in a circle.
Let us consider the triangle IAB.
We know that the sum of the angles in a triangle is $\pi$.
So, we get $\angle AIB+\dfrac{A}{2}+\dfrac{B}{2}=\pi$.
$\Rightarrow \angle AIB=\pi -\dfrac{A+B}{2}$.
We know that the circumradius of triangle PQR is defined as $\dfrac{p}{2\sin P}=\dfrac{q}{2\sin Q}=\dfrac{r}{2\sin R}$.
So, we get ${{P}_{3}}=\dfrac{a}{2\sin \left( \pi -\dfrac{A+B}{2} \right)}$.
We know that $\sin \left( \pi -\alpha \right)=\sin \alpha$.
$\Rightarrow 2{{P}_{3}}=\dfrac{a}{\sin \left( \dfrac{A+B}{2} \right)}$ ---(1).
We know that the sum of angles in triangle ABC is $\pi$.
So, we have $A+B+C=\pi$.
$\Rightarrow A+B=\pi -C$.
$\Rightarrow \dfrac{A+B}{2}=\dfrac{\pi }{2}-\dfrac{C}{2}$ ---(2).
Let us substitute equation (2) in (1).
$\Rightarrow 2{{P}_{3}}=\dfrac{a}{\sin \left( \dfrac{\pi }{2}-\dfrac{C}{2} \right)}$.
We know that $\sin \left( \dfrac{\pi }{2}-\alpha \right)=\cos \alpha$.
$\Rightarrow 2{{P}_{3}}=\dfrac{c}{\cos \left( \dfrac{C}{2} \right)}$.
We know that $\dfrac{1}{\cos \alpha }=\sec \alpha$.
$\Rightarrow 2{{P}_{3}}=c\sec \left( \dfrac{C}{2} \right)$ ---(3).
Similarly, we get $2{{P}_{2}}=b\sec \left( \dfrac{B}{2} \right)$ and $2{{P}_{1}}=a\sec \left( \dfrac{A}{2} \right)$ ---(4).
Now, let us consider $\left( 2{{P}_{1}} \right)\left( 2{{P}_{2}} \right)\left( 2{{P}_{3}} \right)$.
$\Rightarrow 8{{P}_{1}}{{P}_{2}}{{P}_{3}}=\left( a\sec \left( \dfrac{A}{2} \right) \right)\left( b\sec \left( \dfrac{B}{2} \right) \right)\left( c\sec \left( \dfrac{C}{2} \right) \right)$.
We know that $a=2R\sin A$, $b=2R\sin B$ and $c=2R\sin C$, where R is the Circumradius of the triangle ABC.
$\Rightarrow 8{{P}_{1}}{{P}_{2}}{{P}_{3}}=\left( 2R\sin A\sec \left( \dfrac{A}{2} \right) \right)\left( 2R\sin B\sec \left( \dfrac{B}{2} \right) \right)\left( 2R\sin C\sec \left( \dfrac{C}{2} \right) \right)$.
We know that $\sin \alpha =2\sin \left( \dfrac{\alpha }{2} \right)\cos \left( \dfrac{\alpha }{2} \right)$.
$\Rightarrow {{P}_{1}}{{P}_{2}}{{P}_{3}}={{R}^{3}}\left( 2\sin \left( \dfrac{A}{2} \right)\cos \left( \dfrac{A}{2} \right)\sec \left( \dfrac{A}{2} \right) \right)\left( 2\sin \left( \dfrac{B}{2} \right)\cos \left( \dfrac{B}{2} \right)\sec \left( \dfrac{B}{2} \right) \right)\left( 2\sin \left( \dfrac{C}{2} \right)\cos \left( \dfrac{C}{2} \right)\sec \left( \dfrac{C}{2} \right) \right)$.
We know that $\cos \alpha \sec \alpha =1$.
$\Rightarrow {{P}_{1}}{{P}_{2}}{{P}_{3}}=8{{R}^{3}}\left( \sin \left( \dfrac{A}{2} \right) \right)\left( \sin \left( \dfrac{B}{2} \right) \right)\left( \sin \left( \dfrac{C}{2} \right) \right)$.
$\Rightarrow {{P}_{1}}{{P}_{2}}{{P}_{3}}=2{{R}^{2}}\left( 4R\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{B}{2} \right)\sin \left( \dfrac{C}{2} \right) \right)$.
We know that $r=4R\sin \left( \dfrac{A}{2} \right)\sin \left( \dfrac{B}{2} \right)\sin \left( \dfrac{C}{2} \right)$, where r is the inradius of the triangle ABC.
$\Rightarrow {{P}_{1}}{{P}_{2}}{{P}_{3}}=2{{R}^{2}}r$ ---(5).
From equations (3), (4), (5) we have found that all the given options are true.

From equations (3), (4), (5) we have found that all the given options are true.

Note: We can see that the given problem contains a huge amount of calculation so, we have to perform each step carefully in order to avoid confusion and calculation mistakes. We should not confuse the standard notations of the sides and angles of the triangles while solving this problem. Similarly, we can expect problems to find the relation between the exradii of IAB, IBC, ICA and circumradius of ABC.