Solveeit Logo
Login

Question

Question: If \(I=\int\limits_{a}^{b}{\left( {{x}^{4}}-2{{x}^{2}} \right)dx}\) and I is minimum then the ordere...

If I=∫ab(x4−2x2)dxI=\int\limits_{a}^{b}{\left( {{x}^{4}}-2{{x}^{2}} \right)dx} and I is minimum then the ordered pair (a, b) is?
(a) (−2,0)\left( -\sqrt{2},0 \right)
(b) (−2,2)\left( -\sqrt{2},\sqrt{2} \right)
(c) (0,2)\left( 0,\sqrt{2} \right)
(d) (2,−2)\left( \sqrt{2},-\sqrt{2} \right)

Explanation

Solution

First, before proceeding for this, we must suppose the function as f(x) and then we getf(x)=x4−2x2f\left( x \right)={{x}^{4}}-2{{x}^{2}}. Then, to get the ordered pair, we will equate the above as zero. Then, by using the values we got above, we can draw the draw of the curve to get the values of the ordered pair to get the minimum integral value.

Complete step by step answer:
In this question, we are supposed to find the ordered pair (a, b) when I=∫ab(x4−2x2)dxI=\int\limits_{a}^{b}{\left( {{x}^{4}}-2{{x}^{2}} \right)dx}and I is minimum.
So, before proceeding for this, we must suppose the function as f(x) and then we get:
f(x)=x4−2x2f\left( x \right)={{x}^{4}}-2{{x}^{2}}
Now, to get the ordered pair, we will equate the above as zero.
So, by applying this condition, we get:
x4−2x2=0 ⇒x2(x2−2)=0 ⇒x2(x−2)(x+2)=0 \begin{aligned} & {{x}^{4}}-2{{x}^{2}}=0 \\\ & \Rightarrow {{x}^{2}}\left( {{x}^{2}}-2 \right)=0 \\\ & \Rightarrow {{x}^{2}}\left( x-\sqrt{2} \right)\left( x+\sqrt{2} \right)=0 \\\ \end{aligned}
So, we get the values of x as:
x2=0 ⇒x=0,0 \begin{aligned} & {{x}^{2}}=0 \\\ & \Rightarrow x=0,0 \\\ \end{aligned} or x−2=0 ⇒x=2 \begin{aligned} & x-\sqrt{2}=0 \\\ & \Rightarrow x=\sqrt{2} \\\ \end{aligned}or x+2=0 ⇒x=−2 \begin{aligned} & x+\sqrt{2}=0 \\\ & \Rightarrow x=-\sqrt{2} \\\ \end{aligned}
Now, by using the values we got above, we can draw the draw of the curve of the given equation so that we can get the values of the ordered pair which can give minimum or negative value of the integral as:

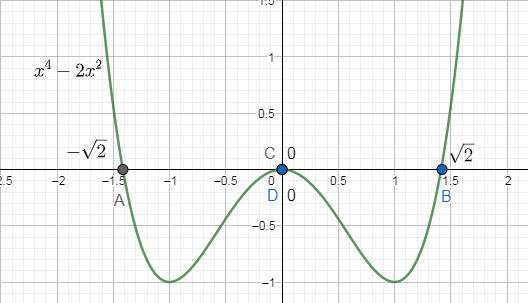
So, we can clearly see from the graph that the minimum of the curves lies between the points AB which gives the range as:
(−2,2)\left( -\sqrt{2},\sqrt{2} \right)
So, we get the minimum integral of I=∫ab(x4−2x2)dxI=\int\limits_{a}^{b}{\left( {{x}^{4}}-2{{x}^{2}} \right)dx} for the ordered pair (−2,2)\left( -\sqrt{2},\sqrt{2} \right).

So, the correct answer is “Option B”.

Note: Now, to solve these types of questions we need to know some of the basic formulas beforehand to solve the question. So, the formulas required to get the answer correctly is as:
(a2−b2)=(a−b)(a+b)\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a-b \right)\left( a+b \right)
Moreover, the arrangement of the ordered pair is also necessary to get the integral positive or negative.