Question

If ${{I}_{1}}$ is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass, and ${{I}_{2}}$ is the moment of inertia (about central axis) of the ring formed by bending the rod, then
$\text{A}\text{. }{{I}_{1}}:{{I}_{2}}=1:1$
$\text{B}\text{. }{{I}_{1}}:{{I}_{2}}={{\pi }^{2}}:3$
$\text{C}\text{. }{{I}_{1}}:{{I}_{2}}=\pi :4$
$\text{D}\text{. }{{I}_{1}}:{{I}_{2}}=3:5$

Answer 1

Consider a small element of dm mass and of dx length, which is at distance of x from the centre of the rod. Use the formula $I=m{{r}^{2}}$. Assume that the rod has uniform mass density and find a relation between dm and dx. Then integrate for the limits from $x=-\dfrac{L}{2}$ to $x=\dfrac{L}{2}$. Repeat the same procedure for the ring.

Formula used:
$I=m{{r}^{2}}$

Complete step-by-step answer:
Let us first derive the expression for both the moments of inertia and then divide both to find the ratio.
Let the mass of the rod be M and length of the rod be L.
For the moment of inertia (${{I}_{1}}$) of the rod about an axis perpendicular to its length and passing through its centre of mass, consider a small element of mass dm. Let the length of this dm mass be dx and let it be at a distance x from the centre of mass of the rod. Assume that the mass of the rod is uniformly distributed and hence the centre of mass will be the centre (midpoint) of the rod.

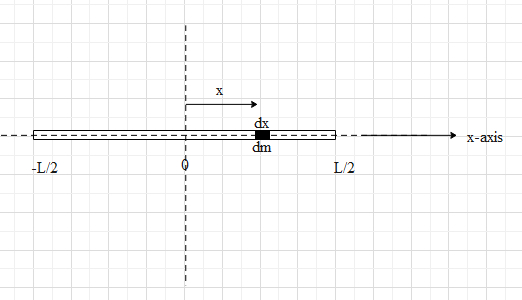
Centre of mass is defined as the product of the mass of the element and its perpendicular distance from the axis of rotation. Here the perpendicular is equal to x. Let the moment of inertia of this element be $d{{I}_{1}}$.
Therefore, $d{{I}_{1}}=dm{{x}^{2}}$ …. (i).
The mass of the rod is uniformly distributed, hence its mass density will be constant.
Therefore, $\dfrac{dm}{dx}=\dfrac{M}{L}$.
$\Rightarrow dm=\dfrac{M}{L}dx$
Substitute the value of dm in equation (i).
$\Rightarrow d{{I}_{1}}=\dfrac{M}{L}{{x}^{2}}dx$.
Integrate both sides and keep the limits of x from $-\dfrac{L}{2}$ to $\dfrac{L}{2}$.
$\Rightarrow \int{d{{I}_{1}}}=\int\limits_{-\dfrac{L}{2}}^{\dfrac{L}{2}}{\dfrac{M}{L}{{x}^{2}}dx}$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\int\limits_{-\dfrac{L}{2}}^{\dfrac{L}{2}}{{{x}^{2}}dx}$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\left. \dfrac{{{x}^{3}}}{3} \right|_{-\dfrac{L}{2}}^{\dfrac{L}{2}}$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\left( \dfrac{{{\left( \dfrac{L}{2} \right)}^{3}}}{3}-\dfrac{{{\left( -\dfrac{L}{2} \right)}^{3}}}{3} \right)$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\left( \dfrac{{{L}^{3}}}{8\times 3}-\dfrac{-{{L}^{3}}}{8\times 3} \right)$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\left( \dfrac{{{L}^{3}}}{8\times 3}+\dfrac{{{L}^{3}}}{8\times 3} \right)=\dfrac{M}{L}\left( \dfrac{2{{L}^{3}}}{8\times 3} \right)$
$\Rightarrow {{I}_{1}}=\dfrac{M}{L}\left( \dfrac{{{L}^{3}}}{4\times 3} \right)=\dfrac{M{{L}^{2}}}{12}$ ….. (ii).
Now the rod is bent to form a circular ring of radius R. Here,$L=2\pi R$ …… (iii).
Now, the axis of rotation is passing through the centre of the ring and is perpendicular to the plane of the ring.
Again consider the mass of the ring. In this case, this dm mass will be at a perpendicular distance of R from the centre.

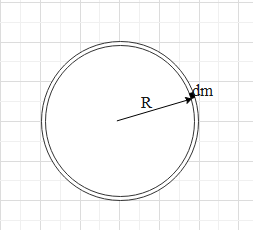
Therefore, $d{{I}_{2}}=dm{{R}^{2}}$
Therefore, ${{I}_{2}}=\int{d{{I}_{2}}}=\int{dm{{R}^{2}}}$
Here, R is constant because the radius of the ring is fixed.
Therefore, ${{I}_{2}}={{R}^{2}}\int{dm}=M{{R}^{2}}$ …… (iv).
Divide equation (i) and equation (iv).
Hence, we get
$\dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{\dfrac{M{{L}^{2}}}{12}}{M{{R}^{2}}}=\dfrac{{{L}^{2}}}{12{{R}^{2}}}$.
Substitute the value of L from equation (iii).
$\Rightarrow \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{(2\pi R)}^{2}}}{12{{R}^{2}}}=\dfrac{4{{\pi }^{2}}{{R}^{2}}}{12{{R}^{2}}}=\dfrac{{{\pi }^{2}}}{3}$
$\Rightarrow {{I}_{1}}:{{I}_{2}}={{\pi }^{2}}:3$

So, the correct answer is “Option B”.

Note: Note that it is not mentioned in the question, but still we have assumed that the rod has a uniform mass density. If the mass has a non-uniform density then the answer will be different. This means that $\dfrac{dm}{dx}$ is not a constant value. Then we must know that variation of mass with respect to the position.