Question

If $h(x) = \underset{n \to \infty}{Lt} \frac{x^{n}f(x)+g(x)+3}{2x^{n}+4x+1}, x \neq 1$ and $h(1) = e^2$ and given that $f(x), g(x), h(x)$ are continuous functions at $x = 1$, then which of the following is/are correct?

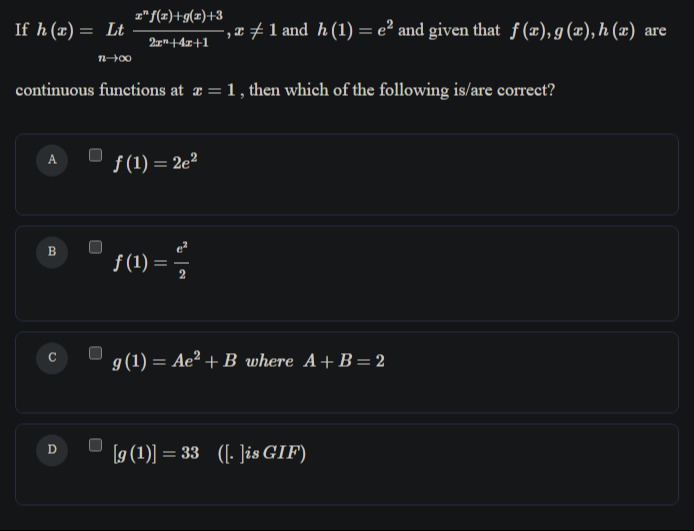
• A. f(1) = 2e²
• B. $f(1) = \frac{e^2}{2}$
• C. $g(1) = Ae^2 + B$ where $A + B = 2$
• D. $[g(1)] = 33$ ([.]is GIF)

Answer 1

Answer: (A), (C), (D)

f(1) = 2e², g(1) = Ae² + B where A + B = 2, [g(1)] = 33

Answer 2

To solve this problem, we need to utilize the concept of continuity of functions and the evaluation of limits involving $x^n$ as $n \to \infty$.

Given:

1. $h(x) = \underset{n \to \infty}{Lt} \frac{x^{n}f(x)+g(x)+3}{2x^{n}+4x+1}$, for $x \neq 1$.
2. $h(1) = e^2$.
3. $f(x)$, $g(x)$, and $h(x)$ are continuous functions at $x = 1$.

The continuity of $h(x)$ at $x=1$ implies that $\underset{x \to 1}{Lt} h(x) = h(1)$.
For the limit to exist, the left-hand limit (LHL) and the right-hand limit (RHL) at $x=1$ must be equal to $h(1)$.
$\underset{x \to 1^-}{Lt} h(x) = \underset{x \to 1^+}{Lt} h(x) = h(1) = e^2$.

Let's evaluate $h(x)$ for different cases of $x$ as $n \to \infty$:

Case 1: For $x \in (0, 1)$ (used for LHL at $x=1$)
When $0 < x < 1$, as $n \to \infty$, $x^n \to 0$.
So, for $x \in (0, 1)$, the expression for $h(x)$ becomes:
$h(x) = \frac{0 \cdot f(x) + g(x) + 3}{2 \cdot 0 + 4x + 1} = \frac{g(x) + 3}{4x + 1}$

Now, we find the left-hand limit of $h(x)$ as $x \to 1^-$:
$\underset{x \to 1^-}{Lt} h(x) = \underset{x \to 1^-}{Lt} \frac{g(x) + 3}{4x + 1}$
Since $g(x)$ is continuous at $x=1$, $\underset{x \to 1^-}{Lt} g(x) = g(1)$.
So, $\underset{x \to 1^-}{Lt} h(x) = \frac{g(1) + 3}{4(1) + 1} = \frac{g(1) + 3}{5}$.

By continuity of $h(x)$ at $x=1$:
$\frac{g(1) + 3}{5} = h(1) = e^2$
$g(1) + 3 = 5e^2$
$g(1) = 5e^2 - 3$

Case 2: For $x > 1$ (used for RHL at $x=1$)
When $x > 1$, as $n \to \infty$, $x^n \to \infty$.
To evaluate the limit, we divide the numerator and denominator by $x^n$:
$h(x) = \underset{n \to \infty}{Lt} \frac{\frac{x^{n}f(x)}{x^n} + \frac{g(x)}{x^n} + \frac{3}{x^n}}{\frac{2x^{n}}{x^n} + \frac{4x}{x^n} + \frac{1}{x^n}} = \underset{n \to \infty}{Lt} \frac{f(x) + \frac{g(x)}{x^n} + \frac{3}{x^n}}{2 + \frac{4x}{x^n} + \frac{1}{x^n}}$
As $n \to \infty$, $\frac{g(x)}{x^n} \to 0$, $\frac{3}{x^n} \to 0$, $\frac{4x}{x^n} \to 0$, $\frac{1}{x^n} \to 0$.
So, for $x > 1$, $h(x) = \frac{f(x)}{2}$.

Now, we find the right-hand limit of $h(x)$ as $x \to 1^+$:
$\underset{x \to 1^+}{Lt} h(x) = \underset{x \to 1^+}{Lt} \frac{f(x)}{2}$
Since $f(x)$ is continuous at $x=1$, $\underset{x \to 1^+}{Lt} f(x) = f(1)$.
So, $\underset{x \to 1^+}{Lt} h(x) = \frac{f(1)}{2}$.

By continuity of $h(x)$ at $x=1$:
$\frac{f(1)}{2} = h(1) = e^2$
$f(1) = 2e^2$

Now let's check the given options:

• f(1) = 2e²
  Our calculated value for $f(1)$ is $2e^2$. So, this option is correct.

• $f(1) = \frac{e^2}{2}$
  This contradicts our calculated value for $f(1)$. So, this option is incorrect.

• $g(1) = Ae^2 + B$ where $A + B = 2$
  Our calculated value for $g(1)$ is $5e^2 - 3$.
  Comparing $5e^2 - 3$ with $Ae^2 + B$, we get $A=5$ and $B=-3$.
  Then $A+B = 5 + (-3) = 2$.
  This satisfies the condition $A+B=2$. So, this option is correct.

• $[g(1)] = 33$ ([.] is GIF)
  We have $g(1) = 5e^2 - 3$.
  Using the approximate value of $e \approx 2.71828$:
  $e^2 \approx (2.71828)^2 \approx 7.389056$
  $g(1) \approx 5(7.389056) - 3$
  $g(1) \approx 36.94528 - 3$
  $g(1) \approx 33.94528$
  The greatest integer function (GIF) of $g(1)$ is $[33.94528] = 33$.
  So, this option is correct.

Therefore, options 1, 3, and 4 are correct.

Explanation of the solution:

The problem uses the concept of continuity, where the limit of the function at a point must equal the function's value at that point. The limit definition of $h(x)$ depends on the value of $x$ relative to 1.

1. For $x \to 1^-$, $x^n \to 0$, simplifying $h(x)$ to $\frac{g(x)+3}{4x+1}$. Using continuity of $g(x)$ and $h(x)$ at $x=1$, we find $g(1) = 5e^2-3$.
2. For $x \to 1^+$, $x^n \to \infty$, simplifying $h(x)$ to $\frac{f(x)}{2}$ by dividing numerator and denominator by $x^n$. Using continuity of $f(x)$ and $h(x)$ at $x=1$, we find $f(1) = 2e^2$.
3. These values are then used to check the given options for correctness.