Question

If g'(x)=f(x), then $\int_{a}^{b} f(x)dx = g(b)-g(a)$.

The value of the integral $\int_{1}^{\infty} (\frac{ln x}{x})^{2018} dx$ is:

• A. $\frac{2018!}{2017^{2018}}$
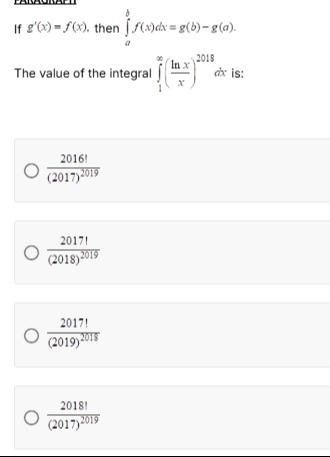
• B. $\frac{2017!}{2018^{2018}}$
• C. $\frac{2017!}{2017^{2019}}$
• D. $\frac{2018!}{2017^{2019}}$

Answer 1

Answer: (D)

$\frac{2018!}{2017^{2019}}$

Answer 2

Let the integral be $I$. We are asked to evaluate $I = \int_{1}^{\infty} \left(\frac{\ln x}{x}\right)^{2018} dx$. Let $n = 2018$. The integral is $I = \int_{1}^{\infty} \left(\frac{\ln x}{x}\right)^n dx$. We use the substitution $u = \ln x$. This implies $x = e^u$ and $dx = e^u du$. When $x=1$, $u = \ln 1 = 0$. As $x \to \infty$, $u \to \infty$. Substituting these into the integral, we get: $I = \int_{0}^{\infty} \left(\frac{u}{e^u}\right)^n e^u du = \int_{0}^{\infty} \frac{u^n}{e^{nu}} e^u du = \int_{0}^{\infty} u^n e^{-(n-1)u} du$.

Now, let $v = (n-1)u$. This implies $u = \frac{v}{n-1}$ and $du = \frac{1}{n-1} dv$. The limits of integration remain $0$ to $\infty$. Substituting these into the integral: $I = \int_{0}^{\infty} \left(\frac{v}{n-1}\right)^n e^{-v} \frac{1}{n-1} dv$ $I = \int_{0}^{\infty} \frac{v^n}{(n-1)^n} e^{-v} \frac{1}{n-1} dv$ $I = \frac{1}{(n-1)^n (n-1)} \int_{0}^{\infty} v^n e^{-v} dv$ $I = \frac{1}{(n-1)^{n+1}} \int_{0}^{\infty} v^n e^{-v} dv$.

The integral $\int_{0}^{\infty} v^n e^{-v} dv$ is the Gamma function $\Gamma(n+1)$. For a positive integer $n$, $\Gamma(n+1) = n!$. Therefore, $I = \frac{1}{(n-1)^{n+1}} \cdot n! = \frac{n!}{(n-1)^{n+1}}$.

In this problem, $n = 2018$. Substituting $n=2018$: $I = \frac{2018!}{(2018-1)^{2018+1}} = \frac{2018!}{2017^{2019}}$.