Question

If $g(x) = x^2 + x - 1$ and $(gof)(x) = 4x^2 - 10x + 5$, then $f(\frac{5}{4})$ is equal to:

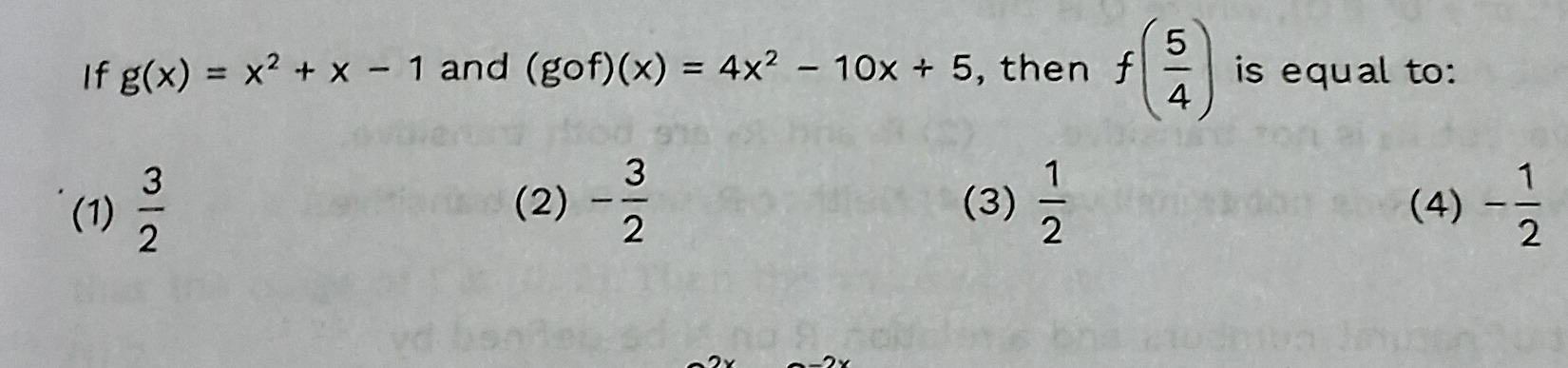
• A. $\frac{3}{2}$
• B. $-\frac{3}{2}$
• C. $\frac{1}{2}$
• D. $-\frac{1}{2}$

Answer 1

Answer: (D)

The correct answer is $-\frac{1}{2}$.

Answer 2

We are given $g(x) = x^2 + x - 1$ and $(g \circ f)(x) = 4x^2 - 10x + 5$. We need to find $f(\frac{5}{4})$.

Since $(g \circ f)(x) = g(f(x))$, we have $g(f(x)) = (f(x))^2 + f(x) - 1$. Thus, $(f(x))^2 + f(x) - 1 = 4x^2 - 10x + 5$.

Substituting $x = \frac{5}{4}$, we get $(f(\frac{5}{4}))^2 + f(\frac{5}{4}) - 1 = 4(\frac{5}{4})^2 - 10(\frac{5}{4}) + 5$.

Simplifying the right side: $4(\frac{25}{16}) - \frac{50}{4} + 5 = \frac{25}{4} - \frac{50}{4} + \frac{20}{4} = \frac{-5}{4}$.

Let $k = f(\frac{5}{4})$. Then $k^2 + k - 1 = -\frac{5}{4}$, which gives $k^2 + k + \frac{1}{4} = 0$.

This factors as $(k + \frac{1}{2})^2 = 0$, so $k = -\frac{1}{2}$.

Therefore, $f(\frac{5}{4}) = -\frac{1}{2}$.