Question

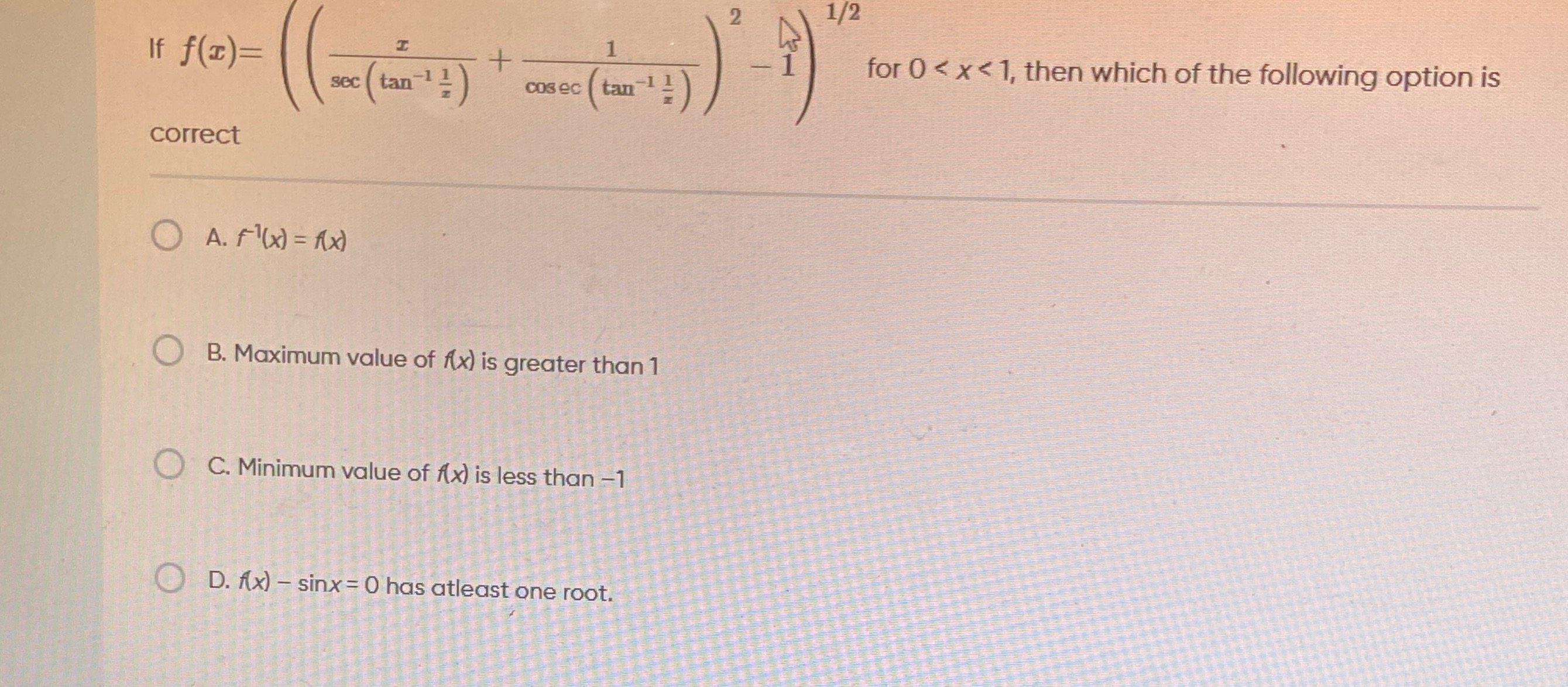
If $f(x)=\left(\left(\frac{x}{\sec\left(\tan^{-1}\frac{1}{x}\right)}+\frac{1}{\csc\left(\tan^{-1}\frac{1}{x}\right)}\right)^2-1\right)^{1/2}$ for $0 < x < 1$, then which of the following option is correct

• A. $f^{-1}(x)=f(x)$
• B. Maximum value of $f(x)$ is greater than 1
• C. Minimum value of $f(x)$ is less than -1
• D. $f(x) - \sin x = 0$ has atleast one root.

Answer 1

Answer: (A)

A. $f^{-1}(x)=f(x)$

Answer 2

The given function is $f(x)=\left(\left(\frac{x}{\sec\left(\tan^{-1}\frac{1}{x}\right)}+\frac{1}{\csc\left(\tan^{-1}\frac{1}{x}\right)}\right)^2-1\right)^{1/2}$ for $0 < x < 1$.

Let $\theta = \tan^{-1}\frac{1}{x}$. Since $0 < x < 1$, $\frac{1}{x} > 1$. The range of $\tan^{-1} y$ for $y > 0$ is $(0, \frac{\pi}{2})$. Since $\frac{1}{x} > 1$, $\theta = \tan^{-1}\frac{1}{x}$ is in the interval $(\frac{\pi}{4}, \frac{\pi}{2})$. In this interval, $\sec\theta > 0$ and $\csc\theta > 0$. We have $\tan\theta = \frac{1}{x}$. We can find $\sec\theta$ and $\csc\theta$ using a right triangle or identities. Using identities: $\sec^2\theta = 1 + \tan^2\theta = 1 + \left(\frac{1}{x}\right)^2 = 1 + \frac{1}{x^2} = \frac{x^2+1}{x^2}$. Since $\theta \in (\frac{\pi}{4}, \frac{\pi}{2})$, $\sec\theta > 0$, so $\sec\theta = \sqrt{\frac{x^2+1}{x^2}} = \frac{\sqrt{x^2+1}}{|x|}$. Since $0 < x < 1$, $|x| = x$. Thus, $\sec\theta = \frac{\sqrt{x^2+1}}{x}$. $\csc^2\theta = 1 + \cot^2\theta = 1 + x^2$. Since $\theta \in (\frac{\pi}{4}, \frac{\pi}{2})$, $\csc\theta > 0$, so $\csc\theta = \sqrt{1+x^2}$.

Now substitute these into the expression for $f(x)$: $\frac{x}{\sec\left(\tan^{-1}\frac{1}{x}\right)} = \frac{x}{\sec\theta} = \frac{x}{\frac{\sqrt{x^2+1}}{x}} = \frac{x^2}{\sqrt{x^2+1}}$. $\frac{1}{\csc\left(\tan^{-1}\frac{1}{x}\right)} = \frac{1}{\csc\theta} = \frac{1}{\sqrt{x^2+1}}$.

The expression inside the square is $\frac{x^2}{\sqrt{x^2+1}} + \frac{1}{\sqrt{x^2+1}} = \frac{x^2+1}{\sqrt{x^2+1}} = \sqrt{x^2+1}$.

So, $f(x) = \left(\left(\sqrt{x^2+1}\right)^2 - 1\right)^{1/2} = \left((x^2+1) - 1\right)^{1/2} = (x^2)^{1/2}$. Since the domain is $0 < x < 1$, $x$ is positive, so $(x^2)^{1/2} = |x| = x$. Thus, $f(x) = x$ for $0 < x < 1$.

Now let's evaluate the given options: A. $f^{-1}(x)=f(x)$ The function is $f(x) = x$ for $x \in (0, 1)$. The domain of $f$ is $(0, 1)$ and the range of $f$ is $(0, 1)$. To find the inverse function, let $y = f(x) = x$. Swap $x$ and $y$: $x = y$. So $y = x$. The domain of $f^{-1}$ is the range of $f$, which is $(0, 1)$. The range of $f^{-1}$ is the domain of $f$, which is $(0, 1)$. So, $f^{-1}(x) = x$ for $x \in (0, 1)$. Therefore, $f^{-1}(x) = f(x)$ for $x \in (0, 1)$. This option is correct.

B. Maximum value of $f(x)$ is greater than 1 $f(x) = x$ for $x \in (0, 1)$. The range of $f(x)$ is $(0, 1)$. The values of $f(x)$ are always strictly between 0 and 1. The supremum is 1, but it is not attained in the open interval. No value of $f(x)$ is greater than 1. This option is incorrect.

C. Minimum value of $f(x)$ is less than -1 $f(x) = x$ for $x \in (0, 1)$. The range of $f(x)$ is $(0, 1)$. The values of $f(x)$ are always strictly positive. The infimum is 0, but it is not attained in the open interval. No value of $f(x)$ is less than -1. This option is incorrect.

D. $f(x) - \sin x = 0$ has atleast one root. This is equivalent to $f(x) = \sin x$, which is $x = \sin x$ for $x \in (0, 1)$. Consider the function $g(x) = x - \sin x$. We are looking for a root of $g(x)$ in the interval $(0, 1)$. We know that for $x > 0$, $\sin x < x$. To prove this, consider $h(x) = x - \sin x$. $h'(x) = 1 - \cos x$. For $x \in (0, 1)$, $0 < x < 1 < \frac{\pi}{2}$, so $\cos x < 1$. Thus $h'(x) = 1 - \cos x > 0$ for $x \in (0, 1)$. Since $h(x)$ is strictly increasing on $(0, 1)$ and $h(0) = 0 - \sin 0 = 0$, for any $x \in (0, 1)$, $h(x) > h(0) = 0$. So $x - \sin x > 0$ for all $x \in (0, 1)$. The equation $x = \sin x$ has no solution in the interval $(0, 1)$. This option is incorrect.

The only correct option is A.