Question
Question: If $F(x)=\int \frac{e^{\cos x}(1+x\sin x)}{x^2}dx$ and $F(\pi)=\frac{-1}{e\pi}$, then $F(\frac{\pi}{...
If F(x)=∫x2ecosx(1+xsinx)dx and F(π)=eπ−1, then F(3π)=
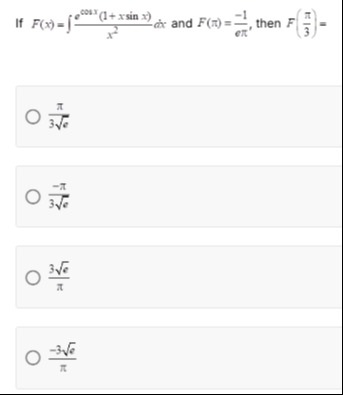
3eπ
3e−π
π3e
π−3e
π−3e
Solution
To find F(3π), we first need to evaluate the indefinite integral F(x)=∫x2ecosx(1+xsinx)dx.
Let's examine the integrand: x2ecosx(1+xsinx). This expression can be rewritten as ecosx(x21+x2xsinx)=ecosx(x21+xsinx).
Consider the derivative of the function xecosx using the quotient rule, dxd(vu)=v2vu′−uv′. Let u=ecosx and v=x. Then u′=dxd(ecosx)=ecosx(−sinx) and v′=dxd(x)=1.
So, dxd(xecosx)=x2x⋅(ecosx(−sinx))−ecosx⋅1=x2−xsinxecosx−ecosx=−x2ecosx(xsinx+1)=−x2ecosx(1+xsinx)
We observe that the integrand given in the problem is exactly the negative of the derivative we just calculated. Therefore, F(x)=∫x2ecosx(1+xsinx)dx=∫−dxd(xecosx)dx F(x)=−xecosx+C where C is the constant of integration.
Now, we use the given condition F(π)=eπ−1 to find the value of C. Substitute x=π into the expression for F(x): F(π)=−πecosπ+C Since cosπ=−1, we have: F(π)=−πe−1+C=−eπ1+C We are given F(π)=eπ−1. So, eπ−1=−eπ1+C This implies C=0.
Thus, the function F(x) is: F(x)=−xecosx
Finally, we need to find F(3π). Substitute x=3π into the expression for F(x): F(3π)=−3πecos(3π) Since cos(3π)=21, we have: F(3π)=−3πe1/2 F(3π)=−3πe F(3π)=−π3e
