Question

If f(x)=2x+|x|, g(x)=$\frac{1}{3}$(2x-|x|) and h(x)=f(g(x)), then domain of function

F(x) = $sin^{-1}$($\underbrace{h(h(h(h....h(x)....)))}_{1000 \text{ times}}$) is equal to which of the following options

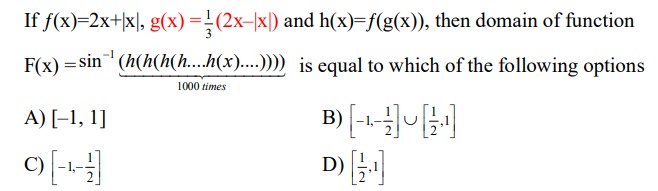
• A. [-1, 1]
• B. [-1, -$\frac{1}{2}$] $\cup$ [$\frac{1}{2}$,1]
• C. [-1,-$\frac{1}{2}$]
• D. [$\frac{1}{2}$,1]

Answer 1

Answer: (A)

[-1, 1]

Answer 2

Let the given functions be $f(x) = 2x + |x|$ and $g(x) = \frac{1}{3}(2x - |x|)$.

We first analyze the functions $f(x)$ and $g(x)$ by considering the two cases for $|x|$.

For $f(x)$: If $x \ge 0$, $|x| = x$, so $f(x) = 2x + x = 3x$. If $x < 0$, $|x| = -x$, so $f(x) = 2x - x = x$. Thus, $f(x) = \begin{cases} 3x & \text{if } x \ge 0 \\ x & \text{if } x < 0 \end{cases}$.

For $g(x)$: If $x \ge 0$, $|x| = x$, so $g(x) = \frac{1}{3}(2x - x) = \frac{1}{3}x$. If $x < 0$, $|x| = -x$, so $g(x) = \frac{1}{3}(2x + x) = x$. Thus, $g(x) = \begin{cases} \frac{1}{3}x & \text{if } x \ge 0 \\ x & \text{if } x < 0 \end{cases}$.

Now we find the function $h(x) = f(g(x))$. We need to consider the cases based on the sign of $x$.

Case 1: $x \ge 0$. In this case, $g(x) = \frac{1}{3}x$. Since $x \ge 0$, $g(x) = \frac{1}{3}x \ge 0$. We use the definition of $f(y)$ for $y \ge 0$, which is $f(y) = 3y$. So, $h(x) = f(g(x)) = f(\frac{1}{3}x) = 3(\frac{1}{3}x) = x$. This holds for $x \ge 0$.

Case 2: $x < 0$. In this case, $g(x) = x$. Since $x < 0$, $g(x) = x < 0$. We use the definition of $f(y)$ for $y < 0$, which is $f(y) = y$. So, $h(x) = f(g(x)) = f(x) = x$. This holds for $x < 0$.

Combining both cases, we find that $h(x) = x$ for all $x \in \mathbb{R}$.

Next, we need to find $h_{1000}(x)$, which is the 1000-fold composition of $h$ with itself. $h_1(x) = h(x) = x$. $h_2(x) = h(h_1(x)) = h(x) = x$. $h_3(x) = h(h_2(x)) = h(x) = x$. By induction, if $h_k(x) = x$, then $h_{k+1}(x) = h(h_k(x)) = h(x) = x$. Therefore, $h_n(x) = x$ for any positive integer $n$. Specifically, $h_{1000}(x) = x$.

The function $F(x)$ is given by $F(x) = \sin^{-1}(h_{1000}(x))$. Substituting $h_{1000}(x) = x$, we get $F(x) = \sin^{-1}(x)$.

The domain of the inverse sine function, $\sin^{-1}(y)$, is $[-1, 1]$. This means the argument of the $\sin^{-1}$ function must lie in the interval $[-1, 1]$. For $F(x) = \sin^{-1}(x)$, the argument is $x$. So, the domain of $F(x)$ is the set of all $x$ such that $x \in [-1, 1]$.

The domain of $F(x)$ is $[-1, 1]$.