Solveeit Logo
Login

Question

Question: If $f(x)+2f(\frac{1}{1-x})=x \space \forall x \in R-\{1\}$ then the value of $27 f(4)$ is...

If f(x)+2f(11−x)=x  ∀x∈R−{1}f(x)+2f(\frac{1}{1-x})=x \space \forall x \in R-\{1\} then the value of 27f(4)27 f(4) is

A

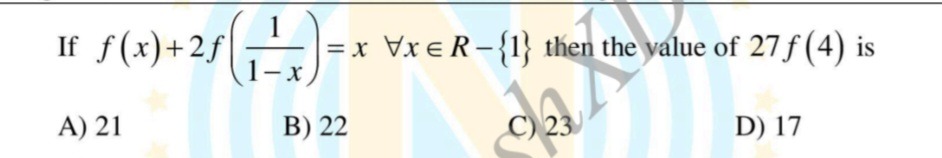
21

B

22

C

23

D

17

Answer

23

Explanation

Solution

The given functional equation is f(x)+2f(11−x)=xf(x)+2f(\frac{1}{1-x})=x for all x∈R−{1}x \in R-\{1\}. We want to find the value of 27f(4)27 f(4).

Let x=4x=4. Substituting this into the given equation, we get: f(4)+2f(11−4)=4f(4) + 2f(\frac{1}{1-4}) = 4 f(4)+2f(−13)=4(1)f(4) + 2f(-\frac{1}{3}) = 4 \quad (1)

Now, let x=−13x = -\frac{1}{3}. Substituting this into the given equation: f(−13)+2f(11−(−13))=−13f(-\frac{1}{3}) + 2f(\frac{1}{1-(-\frac{1}{3})}) = -\frac{1}{3} f(−13)+2f(11+13)=−13f(-\frac{1}{3}) + 2f(\frac{1}{1+\frac{1}{3}}) = -\frac{1}{3} f(−13)+2f(143)=−13f(-\frac{1}{3}) + 2f(\frac{1}{\frac{4}{3}}) = -\frac{1}{3} f(−13)+2f(34)=−13(2)f(-\frac{1}{3}) + 2f(\frac{3}{4}) = -\frac{1}{3} \quad (2)

Next, let x=34x = \frac{3}{4}. Substituting this into the given equation: f(34)+2f(11−34)=34f(\frac{3}{4}) + 2f(\frac{1}{1-\frac{3}{4}}) = \frac{3}{4} f(34)+2f(114)=34f(\frac{3}{4}) + 2f(\frac{1}{\frac{1}{4}}) = \frac{3}{4} f(34)+2f(4)=34(3)f(\frac{3}{4}) + 2f(4) = \frac{3}{4} \quad (3)

We now have a system of three linear equations with three unknowns: f(4)f(4), f(−13)f(-\frac{1}{3}), and f(34)f(\frac{3}{4}). Let A=f(4)A = f(4), B=f(−13)B = f(-\frac{1}{3}), and C=f(34)C = f(\frac{3}{4}). The system of equations becomes:

  1. A+2B=4A + 2B = 4
  2. B+2C=−13B + 2C = -\frac{1}{3}
  3. C+2A=34C + 2A = \frac{3}{4}

We want to find the value of AA. From equation (1), we can express BB in terms of AA: 2B=4−A  ⟹  B=4−A22B = 4 - A \implies B = \frac{4-A}{2}

Substitute this expression for BB into equation (2): 4−A2+2C=−13\frac{4-A}{2} + 2C = -\frac{1}{3} Multiply by 2 to clear the denominator: 4−A+4C=−234-A + 4C = -\frac{2}{3} Now, express 4C4C in terms of AA: 4C=A−4−234C = A - 4 - \frac{2}{3} 4C=A−123−234C = A - \frac{12}{3} - \frac{2}{3} 4C=A−1434C = A - \frac{14}{3} C=A4−1412=A4−76C = \frac{A}{4} - \frac{14}{12} = \frac{A}{4} - \frac{7}{6}

Now substitute this expression for CC into equation (3): (A4−76)+2A=34(\frac{A}{4} - \frac{7}{6}) + 2A = \frac{3}{4} Combine the terms with AA: A4+2A=34+76\frac{A}{4} + 2A = \frac{3}{4} + \frac{7}{6} A+8A4=912+1412\frac{A + 8A}{4} = \frac{9}{12} + \frac{14}{12} 9A4=2312\frac{9A}{4} = \frac{23}{12}

Solve for AA: A=2312×49A = \frac{23}{12} \times \frac{4}{9} A=233×9A = \frac{23}{3 \times 9} A=2327A = \frac{23}{27}

So, f(4)=2327f(4) = \frac{23}{27}. The question asks for the value of 27f(4)27 f(4). 27f(4)=27×2327=2327 f(4) = 27 \times \frac{23}{27} = 23.

The value of 27f(4)27 f(4) is 23.