Question

If $f(x) = x^5 + 2x - 3$, then $(F^{-1})'(-3) =$

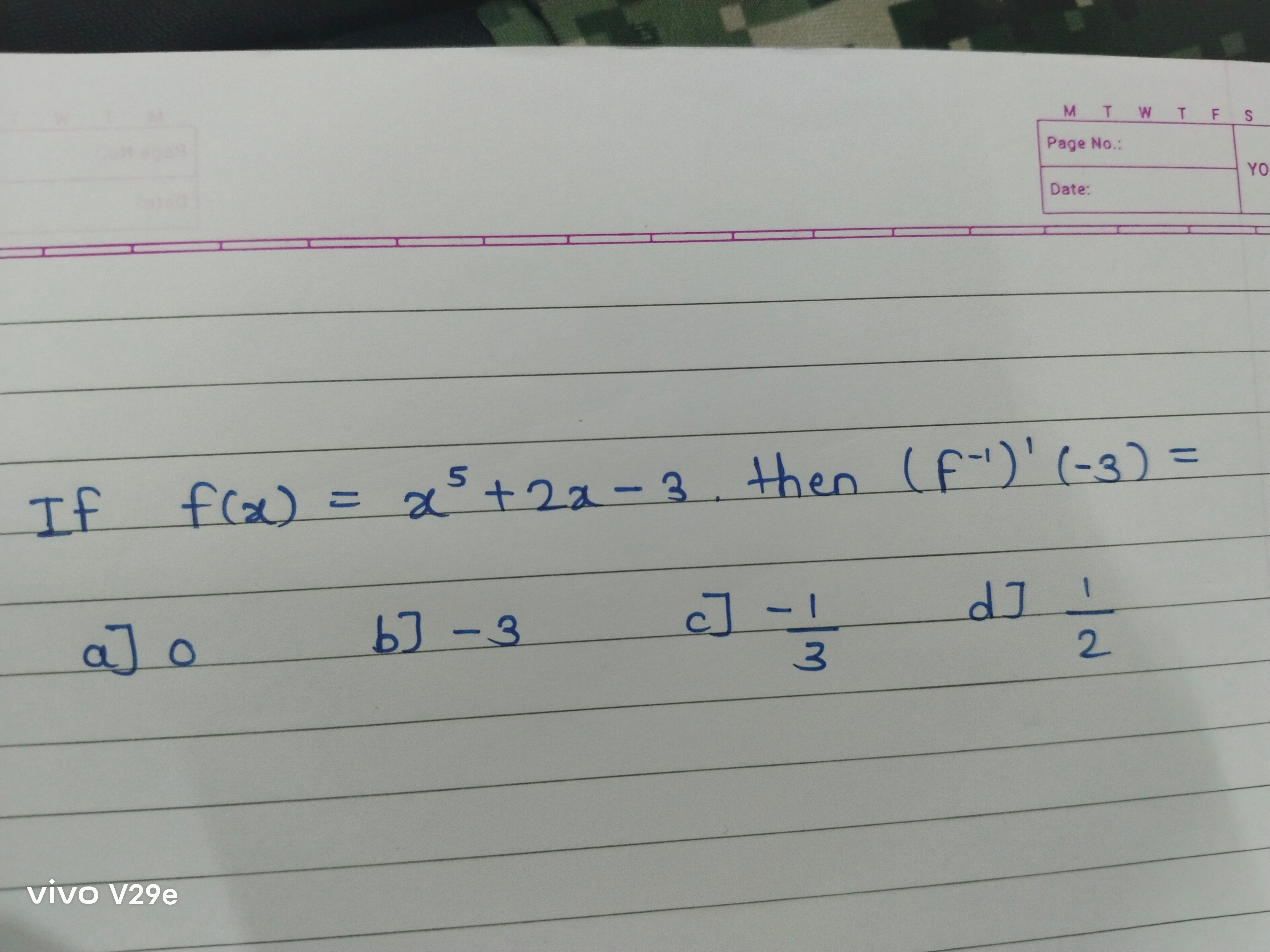
• A. 0
• B. -3
• C. -\frac{1}{3}
• D. \frac{1}{2}

Answer 1

Answer: (D)

\frac{1}{2}

Answer 2

To find $(f^{-1})'(-3)$, we use the formula for the derivative of an inverse function: $(f^{-1})'(y) = \frac{1}{f'(x)}$, where $y = f(x)$.

First, we need to find the value of $x$ such that $f(x) = -3$. $x^5 + 2x - 3 = -3$ $x^5 + 2x = 0$ $x(x^4 + 2) = 0$

The real solution is $x = 0$. We verify this: $f(0) = 0^5 + 2(0) - 3 = -3$.

Next, we find the derivative of $f(x)$: $f'(x) = 5x^4 + 2$

Now, we evaluate $f'(x)$ at $x=0$: $f'(0) = 5(0)^4 + 2 = 2$

Finally, we use the inverse function derivative formula: $(f^{-1})'(-3) = \frac{1}{f'(0)} = \frac{1}{2}$

Therefore, $(F^{-1})'(-3) = \frac{1}{2}$.