Question

If f(x) = $(x^5 + 1)[x^2 - 4x - 5] + sinx + cos(x - 1)]$, then f(x) is not differentiable at -

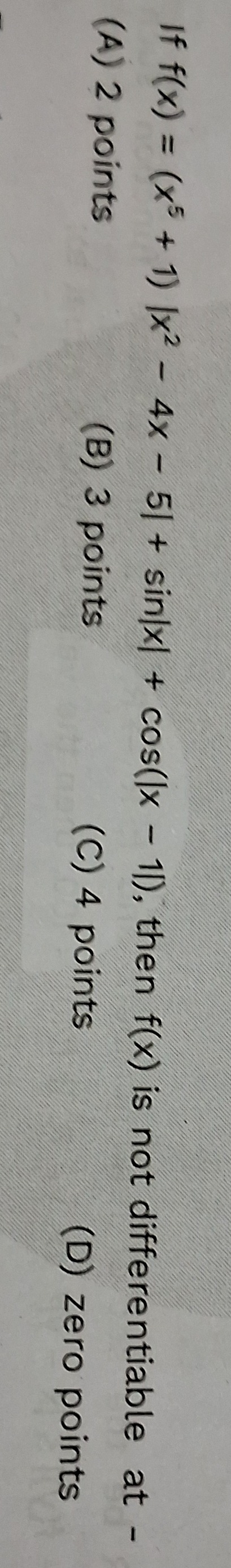
• A. 2 points
• B. 3 points
• C. 4 points
• D. zero points

Answer 1

Answer: (A)

2 points

Answer 2

The function $f(x)$ is not differentiable at points where $x^2 - 4x - 5 = 0$. $x^2 - 4x - 5 = (x-5)(x+1) = 0$, so $x = -1$ or $x = 5$.

At $x = -1$: The left-hand derivative and right-hand derivative of $(x^5 + 1)[x^2 - 4x - 5]$ are different at $x=-1$, so $f(x)$ is not differentiable at $x=-1$.

At $x = 5$: The left-hand derivative and right-hand derivative of $(x^5 + 1)[x^2 - 4x - 5]$ are different at $x=5$, so $f(x)$ is not differentiable at $x=5$.

Therefore, $f(x)$ is not differentiable at 2 points.