Question

If f(x) = $(\tan^{-1}x)^3 + (\tan^{-1}(1/x))^3$, x > 0. Then minimum value of f(x) is

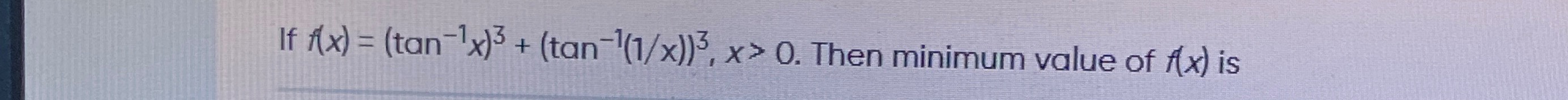
• A. $\frac{\pi^3}{32}$
• B. $\frac{\pi^3}{64}$
• C. $\frac{\pi^3}{16}$
• D. $\frac{\pi^3}{8}$

Answer 1

Answer: (A)

$\frac{\pi^3}{32}$

Answer 2

Let $a = \tan^{-1}x$. For $x > 0$, we have $a \in (0, \pi/2)$. Using the identity $\tan^{-1}x + \tan^{-1}(1/x) = \pi/2$, we get $\tan^{-1}(1/x) = \pi/2 - a$. The function becomes $f(x) = g(a) = a^3 + (\pi/2 - a)^3$. We need to find the minimum value of $g(a)$ for $a \in (0, \pi/2)$. The function $g(a)$ is a sum of cubes. For a fixed sum $a + (\pi/2 - a) = \pi/2$, the sum of cubes $a^3 + (\pi/2 - a)^3$ is minimized when $a$ and $\pi/2 - a$ are equal, i.e., $a = \pi/2 - a$, which gives $a = \pi/4$. This value is in the domain $(0, \pi/2)$. The minimum value is obtained by substituting $a = \pi/4$ into the expression for $g(a)$, which gives $(\pi/4)^3 + (\pi/2 - \pi/4)^3 = (\pi/4)^3 + (\pi/4)^3 = 2(\pi/4)^3 = 2 \cdot \frac{\pi^3}{64} = \frac{\pi^3}{32}$.