Question
Question: If $f(x) = \tan^{-1}(\frac{\sqrt{1+x^2}-1}{x})$ then $f'(0)$ is:...
If f(x)=tan−1(x1+x2−1) then f′(0) is:
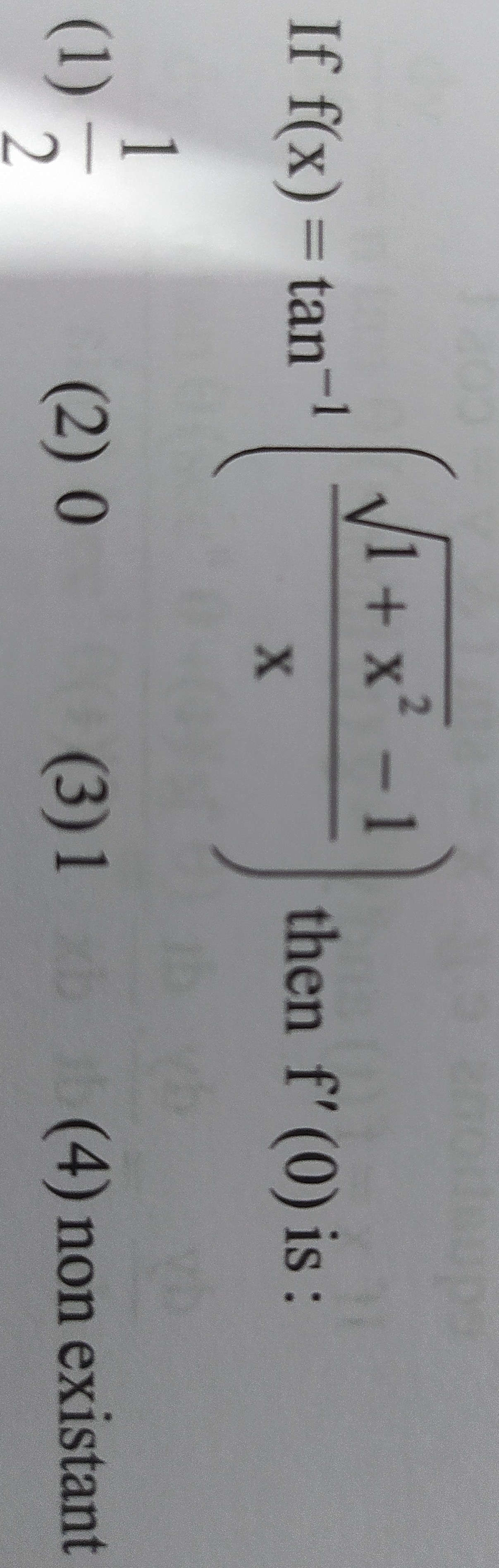
21
0
1
non existant
1/2
Solution
To find f′(0) for f(x)=tan−1(x1+x2−1), we first simplify the expression for f(x).
Step 1: Simplify the expression inside the tan−1 function.
Let x=tanθ. Since the domain of tan−1x is (−∞,∞), θ=tan−1x implies θ∈(−π/2,π/2).
Substitute x=tanθ into the expression:
x1+x2−1=tanθ1+tan2θ−1We know that 1+tan2θ=sec2θ.
=tanθsec2θ−1Since θ∈(−π/2,π/2), cosθ>0, which means secθ>0. Therefore, sec2θ=∣secθ∣=secθ.
=tanθsecθ−1Convert secθ and tanθ to sinθ and cosθ:
=cosθsinθcosθ1−1=cosθsinθcosθ1−cosθ=sinθ1−cosθNow, use the half-angle trigonometric identities: 1−cosθ=2sin2(θ/2) and sinθ=2sin(θ/2)cos(θ/2).
=2sin(θ/2)cos(θ/2)2sin2(θ/2)=cos(θ/2)sin(θ/2)=tan(θ/2)Step 2: Determine the simplified form of f(x).
Substitute the simplified expression back into f(x):
f(x)=tan−1(tan(θ/2))Since θ∈(−π/2,π/2), it follows that θ/2∈(−π/4,π/4).
For any y∈(−π/2,π/2), tan−1(tany)=y. Since θ/2∈(−π/4,π/4), which is a subinterval of (−π/2,π/2), we have:
f(x)=θ/2Now, substitute back θ=tan−1x:
f(x)=21tan−1xThis simplified form is valid for all x∈R.
For x=0, the original function's argument is 01+02−1=00, which is an indeterminate form.
We evaluate the limit: limx→0x1+x2−1=limx→0x(1+x2+1)(1+x2−1)(1+x2+1)=limx→0x(1+x2+1)1+x2−1=limx→0x(1+x2+1)x2=limx→01+x2+1x=1+10=0.
So, f(0)=tan−1(0)=0.
The simplified form f(x)=21tan−1x also gives f(0)=21tan−1(0)=0. Thus, f(x)=21tan−1x is valid for all x.
Step 3: Calculate the derivative f′(x).
Differentiate f(x)=21tan−1x with respect to x:
f′(x)=dxd(21tan−1x)=21⋅1+x21Step 4: Evaluate f′(0).
Substitute x=0 into f′(x):
f′(0)=21⋅1+021=21⋅11=21