Question
Question: If f(x) = sgn(x$^5$), then which of the following is/are false (where sgn denotes signum function):...
If f(x) = sgn(x5), then which of the following is/are false (where sgn denotes signum function):
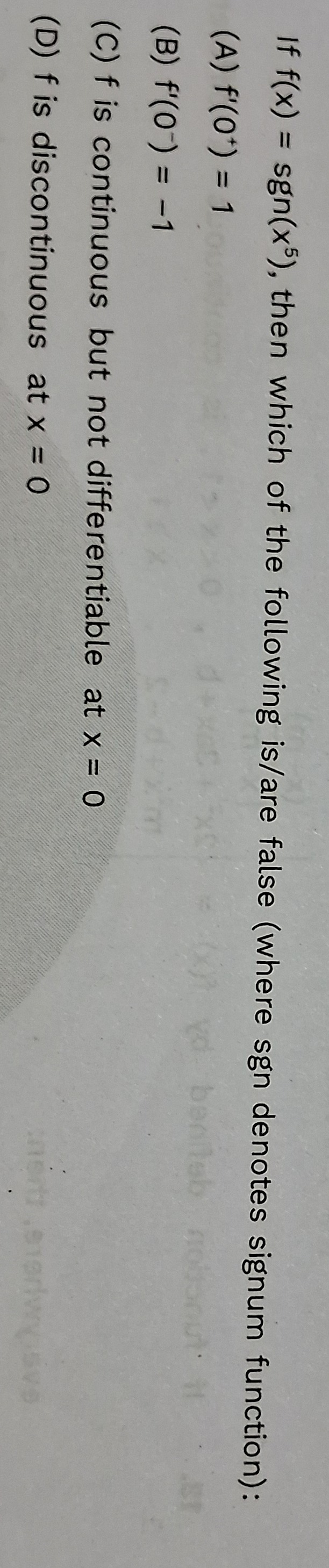
f'(0+) = 1
f'(0) = -1
f is continuous but not differentiable at x = 0
f is discontinuous at x = 0
(A), (B), (C)
Solution
The given function is f(x)=sgn(x5).
The signum function sgn(u) is defined as:
sgn(u)=⎩⎨⎧10−1if u>0if u=0if u<0Let's analyze f(x) based on the value of x5:
- If x>0, then x5>0, so f(x)=sgn(x5)=1.
- If x=0, then x5=0, so f(x)=sgn(x5)=0.
- If x<0, then x5<0, so f(x)=sgn(x5)=−1.
Thus, f(x) can be simplified to:
f(x)=⎩⎨⎧10−1if x>0if x=0if x<0This is precisely the definition of the signum function sgn(x). So, f(x)=sgn(x).
Now, let's evaluate the continuity and differentiability of f(x) at x=0.
Continuity at x=0:
For f(x) to be continuous at x=0, we must have limx→0−f(x)=limx→0+f(x)=f(0).
- Left-hand limit (LHL):
limx→0−f(x)=limx→0−(−1)=−1. - Right-hand limit (RHL):
limx→0+f(x)=limx→0+(1)=1. - Function value at x=0:
f(0)=0.
Since LHL (=−1) is not equal to RHL (=1), the limit of f(x) as x→0 does not exist. Therefore, f(x) is discontinuous at x=0.
Differentiability at x=0:
A function must be continuous at a point to be differentiable at that point. Since f(x) is discontinuous at x=0, it is not differentiable at x=0.
Now let's check each statement:
(A) f'(0+) = 1
This refers to the right-hand derivative at x=0.
f′(0+)=limh→0+hf(0+h)−f(0)
For h>0, f(h)=1 and f(0)=0.
f′(0+)=limh→0+h1−0=limh→0+h1=∞.
Since ∞=1, statement (A) is false.
(B) f'(0) = -1
As established, f(x) is not differentiable at x=0. Therefore, f′(0) does not exist.
Since f′(0) does not exist, it cannot be equal to −1. Statement (B) is false.
(C) f is continuous but not differentiable at x = 0
We have determined that f is discontinuous at x=0.
Therefore, the first part of the statement, "f is continuous at x = 0", is false. This makes the entire compound statement false.
(D) f is discontinuous at x = 0
We have determined that f is discontinuous at x=0.
Therefore, statement (D) is true.
The question asks for the statements that are false. Based on our analysis, statements (A), (B), and (C) are false.
