Solveeit Logo
Login

Question

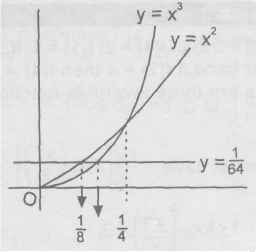
Question: If f(x) = maximum \(\left\{ x ^ { 3 } , x ^ { 2 } , \frac { 1 } { 64 } \right\}\)∀ x ∈\[0, ∞), then...

If f(x) = maximum {x3,x2,164}\left\{ x ^ { 3 } , x ^ { 2 } , \frac { 1 } { 64 } \right\}∀ x ∈[0, ∞), then

A

f(x) = {x2,0≤x≤1x3,x>1\left\{ \begin{array} { c c } x ^ { 2 } , & 0 \leq x \leq 1 \\ x ^ { 3 } , & x > 1 \end{array} \right.

B

f(x) = {164,0≤x≤14x2,14<x≤1x3,x>1\left\{ \begin{array} { c c } \frac { 1 } { 64 } , & 0 \leq x \leq \frac { 1 } { 4 } \\ x ^ { 2 } , & \frac { 1 } { 4 } < x \leq 1 \\ x ^ { 3 } , & x > 1 \end{array} \right.

C

f(x) =

D

f(x) =

Answer

f(x) =

Explanation

Solution

Clearly f(x) =