Question

If f(x) is an odd continuous function in [-2, 2] and differentiable in (-2, 2), then:

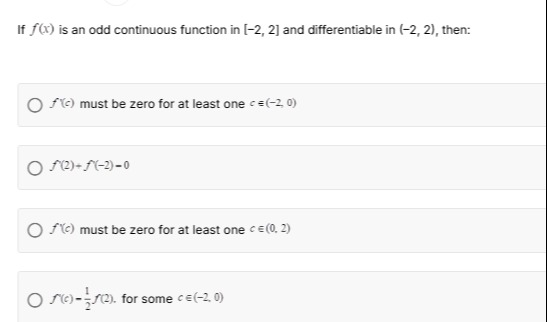
• A. f'(c) must be zero for at least one c in (-2, 0)
• B. f'(2)+f'(-2)=0
• C. f'(c) must be zero for at least one c in (0, 2)
• D. f'(c)=1/2 * f(2), for some c in (-2, 0)

Answer 1

Answer: (D)

f'(c)=1/2 * f(2), for some c in (-2, 0)

Answer 2

Given that $f(x)$ is an odd function, we know that $f(-x) = -f(x)$ for all $x$ in its domain. Differentiating both sides with respect to $x$, we get: $\frac{d}{dx} f(-x) = \frac{d}{dx} (-f(x))$ Using the chain rule on the left side: $f'(-x) \cdot (-1) = -f'(x)$ $-f'(-x) = -f'(x)$ $f'(-x) = f'(x)$ This shows that the derivative $f'(x)$ is an even function.

Also, for an odd function, $f(0) = 0$. This is because $f(-0) = -f(0)$, which implies $f(0) = -f(0)$, so $2f(0) = 0$, hence $f(0) = 0$.

Now let's analyze the options:

• Option 1 & 3: For $f(x) = x$, which is an odd, continuous, and differentiable function, its derivative is $f'(x) = 1$. This derivative is never zero for any $c$ in $(-2, 0)$ or $(0, 2)$. Thus, these statements are false.

• Option 2: $f'(2) + f'(-2) = 0$. Since $f'(x)$ is an even function, $f'(-2) = f'(2)$. Substituting this into the equation gives: $f'(2) + f'(2) = 0$ $2f'(2) = 0$ $f'(2) = 0$ This implies that the derivative of any odd function must be zero at $x=2$. Consider $f(x) = x^3$. This is an odd function, and its derivative is $f'(x) = 3x^2$. At $x=2$, $f'(2) = 3(2^2) = 12 \neq 0$. Thus, this statement is false.

• Option 4: $f'(c) = \frac{1}{2}f(2)$, for some $c \in (-2, 0)$. We can apply the Mean Value Theorem (MVT) to the function $f(x)$ on the interval $[-2, 0]$. Since $f(x)$ is continuous on $[-2, 0]$ and differentiable on $(-2, 0)$, the MVT guarantees that there exists at least one $c \in (-2, 0)$ such that: $f'(c) = \frac{f(0) - f(-2)}{0 - (-2)}$ We know $f(0) = 0$ and, since $f$ is odd, $f(-2) = -f(2)$. Substituting these values: $f'(c) = \frac{0 - (-f(2))}{0 - (-2)} = \frac{f(2)}{2}$ This matches the statement in Option 4. Therefore, this statement is true.