Question
Question: If $f(x) = \int_{0}^{\frac{\pi}{2}} \frac{\ln(1+x\sin^2\theta)}{\sin^2\theta} d\theta, x\ge 0$, then...
If f(x)=∫02πsin2θln(1+xsin2θ)dθ,x≥0, then f′(3)π equals
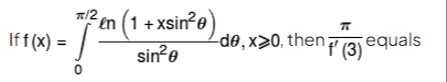
4
Solution
Let the given function be f(x)=∫02πsin2θln(1+xsin2θ)dθ for x≥0. We need to find the value of f′(3)π.
First, we find the derivative of f(x) with respect to x using Leibniz rule for differentiation under the integral sign. The rule states that if f(x)=∫abh(x,θ)dθ, where a and b are constants, then f′(x)=∫ab∂x∂h(x,θ)dθ. In our case, h(x,θ)=sin2θln(1+xsin2θ), a=0, and b=2π. The partial derivative of h(x,θ) with respect to x is: ∂x∂(sin2θln(1+xsin2θ))=sin2θ1⋅∂x∂(ln(1+xsin2θ)) Using the chain rule, ∂x∂(ln(1+xsin2θ))=1+xsin2θ1⋅∂x∂(1+xsin2θ)=1+xsin2θ1⋅sin2θ. So, ∂x∂h(x,θ)=sin2θ1⋅1+xsin2θsin2θ=1+xsin2θ1. Thus, f′(x)=∫02π1+xsin2θ1dθ.
Now, we need to evaluate this integral. Let I(x)=∫02π1+xsin2θ1dθ. We can divide the numerator and denominator by cos2θ: I(x)=∫02πsec2θ+xtan2θsec2θdθ. Using the identity sec2θ=1+tan2θ: I(x)=∫02π1+tan2θ+xtan2θsec2θdθ=∫02π1+(1+x)tan2θsec2θdθ. Let u=tanθ. Then du=sec2θdθ. When θ=0, u=tan(0)=0. When θ=2π, u=tan(2π)=∞. The integral becomes: I(x)=∫0∞1+(1+x)u2du. We can write the denominator as 1+(1+xu)2. Let v=1+xu. Then dv=1+xdu, so du=1+xdv. When u=0, v=0. When u=∞, v=∞. The integral becomes: I(x)=∫0∞1+v211+xdv=1+x1∫0∞1+v2dv. The integral ∫0∞1+v2dv is a standard integral: ∫0∞1+v2dv=[arctan(v)]0∞=arctan(∞)−arctan(0)=2π−0=2π. So, I(x)=1+x1⋅2π=21+xπ. Thus, f′(x)=21+xπ.
We need to find the value of f′(3)π. First, we find f′(3) by substituting x=3 into the expression for f′(x): f′(3)=21+3π=24π=2⋅2π=4π.
Finally, we calculate f′(3)π: f′(3)π=4ππ=π⋅π4=4.
The final answer is 4.
Explanation:
- Use Leibniz rule to differentiate f(x) under the integral sign.
- The derivative f′(x) is found to be ∫02π1+xsin2θ1dθ.
- Evaluate the integral by transforming it using trigonometric identities and substitution (tanθ).
- The integral evaluates to 21+xπ, so f′(x)=21+xπ.
- Calculate f′(3) by substituting x=3 into the expression for f′(x).
- f′(3)=4π.
- Calculate the required value f′(3)π=4ππ=4.
