Question
Question: If $f(x) = \begin{vmatrix} (x-3)e^x & x & \sin x \\ (x-2)e^x & 1 & \cos x \\ (x-1)e^x & 0 & -\sin x ...
If f(x)=(x−3)ex(x−2)ex(x−1)exx10sinxcosx−sinx then the value of Ltx→0∣xf(x)∣ is equal to
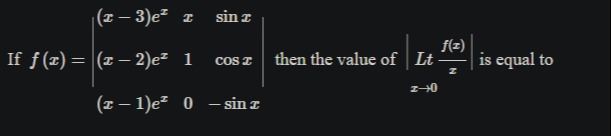
3
Solution
To find the value of Ltx→0∣xf(x)∣, we first need to evaluate the determinant f(x).
Given f(x)=(x−3)ex(x−2)ex(x−1)exx10sinxcosx−sinx
Step 1: Evaluate the determinant f(x). We can factor out ex from the first column (C1): f(x)=exx−3x−2x−1x10sinxcosx−sinx
Now, let's expand the determinant along the second column (C2) because it contains a zero, which simplifies the calculation: f(x)=ex[−xx−2x−1cosx−sinx+1x−3x−1sinx−sinx−0x−3x−2sinxcosx]
Calculate the 2×2 determinants: x−2x−1cosx−sinx=(x−2)(−sinx)−(x−1)cosx=−(x−2)sinx−(x−1)cosx x−3x−1sinx−sinx=(x−3)(−sinx)−(x−1)sinx=−(x−3)sinx−(x−1)sinx
Substitute these back into the expression for f(x): f(x)=ex[−x(−(x−2)sinx−(x−1)cosx)+(−(x−3)sinx−(x−1)sinx)] f(x)=ex[x(x−2)sinx+x(x−1)cosx−(x−3+x−1)sinx] f(x)=ex[(x2−2x)sinx+(x2−x)cosx−(2x−4)sinx] Combine the terms with sinx: f(x)=ex[(x2−2x−2x+4)sinx+(x2−x)cosx] f(x)=ex[(x2−4x+4)sinx+(x2−x)cosx] Recognize the perfect square: (x2−4x+4)=(x−2)2. f(x)=ex[(x−2)2sinx+x(x−1)cosx]
Step 2: Simplify the expression xf(x). xf(x)=xex[(x−2)2sinx+x(x−1)cosx] Divide each term in the bracket by x: xf(x)=ex[x(x−2)2sinx+xx(x−1)cosx] xf(x)=ex[(x−2)2xsinx+(x−1)cosx]
Step 3: Evaluate the limit Ltx→0xf(x). Now, we apply the limit x→0: Ltx→0xf(x)=Ltx→0ex[(x−2)2xsinx+(x−1)cosx]
Using the properties of limits and standard limits:
- Ltx→0ex=e0=1
- Ltx→0(x−2)2=(0−2)2=4
- Ltx→0xsinx=1 (Standard limit)
- Ltx→0(x−1)=(0−1)=−1
- Ltx→0cosx=cos0=1
Substitute these values into the limit expression: Ltx→0xf(x)=1[(4)(1)+(−1)(1)] Ltx→0xf(x)=1[4−1] Ltx→0xf(x)=3
Step 4: Take the absolute value. The question asks for Ltx→0∣xf(x)∣. Ltx→0∣xf(x)∣=∣3∣=3.
The final answer is 3.
