Question
Question: If $f(x) = \begin{vmatrix} \cos{(x + x^2)} & \sin{(x + x^2)} & -\cos{(x + x^2)} \\ \sin{(x - x^2)} &...
If f(x)=cos(x+x2)sin(x−x2)sin2xsin(x+x2)cos(x−x2)0−cos(x+x2)sin(x−x2)sin2x2, then
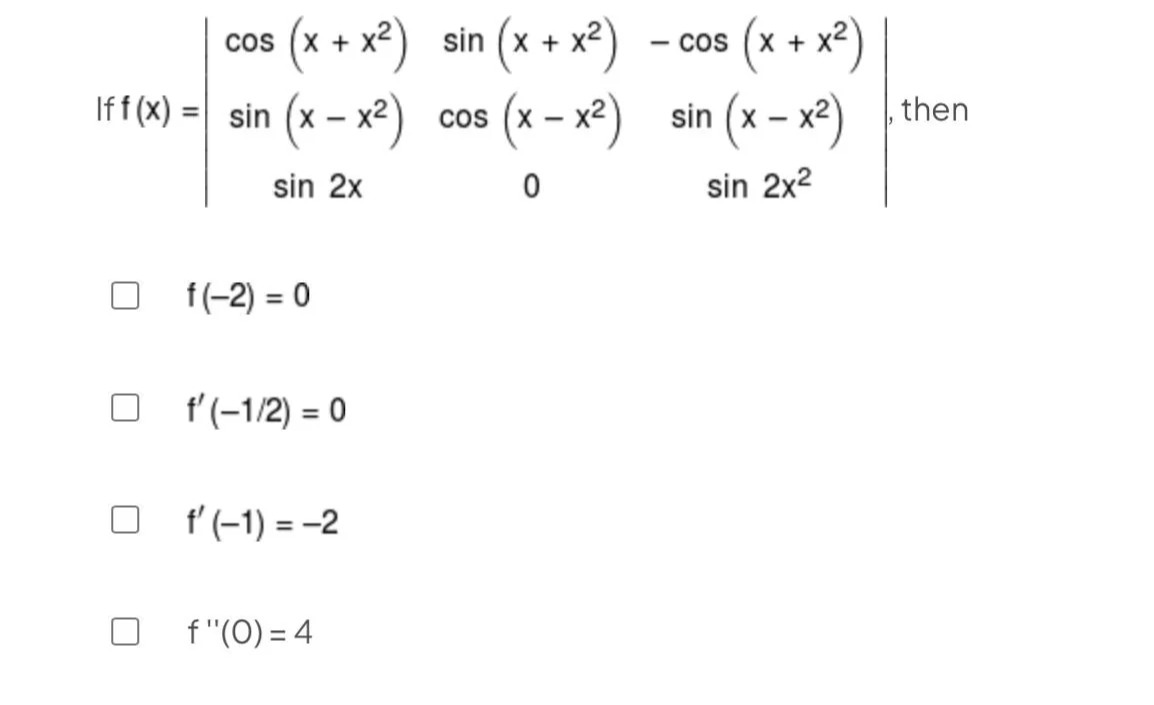
f(-2) = 0
f'(-1/2) = 0
f' (-1) = -2
f ''(0) = 4
f'(-1/2) = 0, f' (-1) = -2, f ''(0) = 4
Solution
We start with
f(x)=cos(x+x2)sin(x−x2)sin2xsin(x+x2)cos(x−x2)0−cos(x+x2)sin(x−x2)sin2x2.Let
u=x+x2,v=x−x2,and write A=cosu,B=sinu,C=sinv,D=cosv,E=sin2x,F=sin2x2.Then the matrix becomes
ACEBD0−ACF.Perform the column operation: replace the 3rd column by (Column 1 + Column 3). Then
C3→C1+C3:ACEBD0A−A=0C+C=2CE+F.Now expanding the determinant along the first row (since the 1st row, 3rd entry is 0):
f(x)=Adet(D02CE+F)−Bdet(CE2CE+F).This gives
f(x)=A[D(E+F)]−B[C(E+F)−2CE]=AD(E+F)−BC(F−E).Now using the trigonometric identities
cosucosv−sinusinv=cos(u+v),cosucosv+sinusinv=cos(u−v),we write
f(x)=E[cosucosv+sinusinv]+F[cosucosv−sinusinv]=Ecos(u−v)+Fcos(u+v).But note that
u−v=(x+x2)−(x−x2)=2x2,u+v=(x+x2)+(x−x2)=2x.So we have
f(x)=sin2xcos2x2+sin2x2cos2x.Using the sine addition formula
sinαcosβ+cosαsinβ=sin(α+β),with α=2x and β=2x2, we obtain
f(x)=sin(2x+2x2).Now we check the options:
-
f(−2):
f(−2)=sin(2(−2)+2(−2)2)=sin(−4+8)=sin(4) which is generally nonzero. -
f′(−21):
f′(x)=cos(2x+2x2)(2+4x).
Differentiating,Thus,
f′(−21)=cos(2(−21)+2(41))(2+4(−21))=cos(−1+0.5)(2−2)=cos(−0.5)⋅0=0. -
f′(−1):
f′(−1)=cos(2(−1)+2(1))(2+4(−1))=cos(−2+2)(2−4)=cos(0)⋅(−2)=1⋅(−2)=−2. -
f′′(0):
f′(x)=cos(2x+2x2)(2+4x).
First, f(0)=sin(0)=0.
We haveThen,
f′′(x)=−sin(2x+2x2)(2+4x)2+4cos(2x+2x2).At x=0 we get
f′′(0)=−sin(0)⋅(2)2+4cos(0)=0+4⋅1=4.
Thus, the correct statements are options 2, 3, and 4.
