Question

If f(x) = $\begin{cases} max\{[x],x\} ; & 0<x<\frac{\pi}{4} \\ b; & x = 0 \\ min\{sin x, cos x\}; & -\frac{\pi}{4}<x<0 \end{cases}$ is continuous at x = 0, then f'(0) is (where [.] represents greatest integer function)

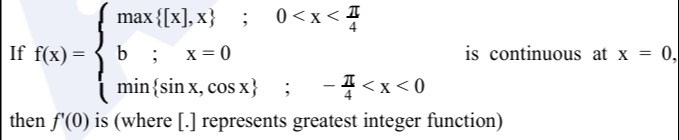
Answer 1

1

Answer 2

The problem asks us to find the derivative of a piecewise function at $x=0$, given that the function is continuous at $x=0$.

Step 1: Determine the value of 'b' using the continuity condition at x = 0. For a function $f(x)$ to be continuous at $x=0$, the following condition must be met: $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^+} f(x) = f(0)$

1. Evaluate $f(0)$: From the given definition, $f(0) = b$.

2. Evaluate the right-hand limit, $\lim_{x \to 0^+} f(x)$: For $0 < x < \frac{\pi}{4}$, $f(x) = \max\{[x], x\}$. Since $0 < x < \frac{\pi}{4}$ (which is approximately $0 < x < 0.785$), $x$ is in the interval $(0, 1)$. For any $x \in (0, 1)$, the greatest integer less than or equal to $x$, $[x]$, is $0$. So, for $0 < x < \frac{\pi}{4}$, $f(x) = \max\{0, x\}$. Since $x > 0$ in this interval, $\max\{0, x\} = x$. Therefore, $\lim_{x \to 0^+} f(x) = \lim_{x \to 0^+} x = 0$.

3. Evaluate the left-hand limit, $\lim_{x \to 0^-} f(x)$: For $-\frac{\pi}{4} < x < 0$, $f(x) = \min\{\sin x, \cos x\}$. In the interval $(-\frac{\pi}{4}, 0)$, $x$ lies in the fourth quadrant. In the fourth quadrant:

   • $\sin x < 0$ (sine is negative)
   • $\cos x > 0$ (cosine is positive) Since $\sin x$ is negative and $\cos x$ is positive, it must be that $\sin x < \cos x$. So, for $-\frac{\pi}{4} < x < 0$, $f(x) = \min\{\sin x, \cos x\} = \sin x$. Therefore, $\lim_{x \to 0^-} f(x) = \lim_{x \to 0^-} \sin x = \sin(0) = 0$.

4. Apply the continuity condition: From the above evaluations, we have $b = 0 = 0$. Thus, the value of $b$ is $0$.

Now, the function $f(x)$ can be written as: $f(x) = \begin{cases} x ; & 0<x<\frac{\pi}{4} \\ 0; & x = 0 \\ \sin x; & -\frac{\pi}{4}<x<0 \end{cases}$

Step 2: Calculate $f'(0)$ using the definition of the derivative. For $f'(0)$ to exist, the left-hand derivative ($f'(0^-)$) and the right-hand derivative ($f'(0^+)$) must exist and be equal.

1. Calculate the right-hand derivative, $f'(0^+)$: $f'(0^+) = \lim_{h \to 0^+} \frac{f(0+h) - f(0)}{h}$ For small $h > 0$, $f(h) = h$ (from the first case of the function definition). $f(0) = 0$. $f'(0^+) = \lim_{h \to 0^+} \frac{h - 0}{h} = \lim_{h \to 0^+} 1 = 1$.

2. Calculate the left-hand derivative, $f'(0^-)$: $f'(0^-) = \lim_{h \to 0^-} \frac{f(0+h) - f(0)}{h}$ For small $h < 0$, $f(h) = \sin(h)$ (from the third case of the function definition). $f(0) = 0$. $f'(0^-) = \lim_{h \to 0^-} \frac{\sin(h) - 0}{h} = \lim_{h \to 0^-} \frac{\sin(h)}{h}$. This is a standard limit, which evaluates to $1$. $f'(0^-) = 1$.

3. Conclusion: Since $f'(0^+) = f'(0^-) = 1$, the derivative $f'(0)$ exists and is equal to $1$.

The final answer is $\boxed{1}$.

Explanation of the solution:

1. Continuity at x=0: The limits from the left and right, and the function value at $x=0$, must be equal.
   • For $0 < x < \frac{\pi}{4}$, $[x]=0$, so $f(x) = \max\{0,x\} = x$. $\lim_{x \to 0^+} f(x) = 0$.
   • For $-\frac{\pi}{4} < x < 0$, $\sin x < \cos x$, so $f(x) = \min\{\sin x, \cos x\} = \sin x$. $\lim_{x \to 0^-} f(x) = \sin(0) = 0$.
   • Given $f(0)=b$. For continuity, $0 = 0 = b$, so $b=0$.
2. Differentiability at x=0: The left-hand derivative and right-hand derivative must be equal.
   • Right-hand derivative: $f'(0^+) = \lim_{h \to 0^+} \frac{f(h)-f(0)}{h} = \lim_{h \to 0^+} \frac{h-0}{h} = 1$.
   • Left-hand derivative: $f'(0^-) = \lim_{h \to 0^-} \frac{f(h)-f(0)}{h} = \lim_{h \to 0^-} \frac{\sin h - 0}{h} = 1$.
   • Since both derivatives are equal to 1, $f'(0)=1$.