Question
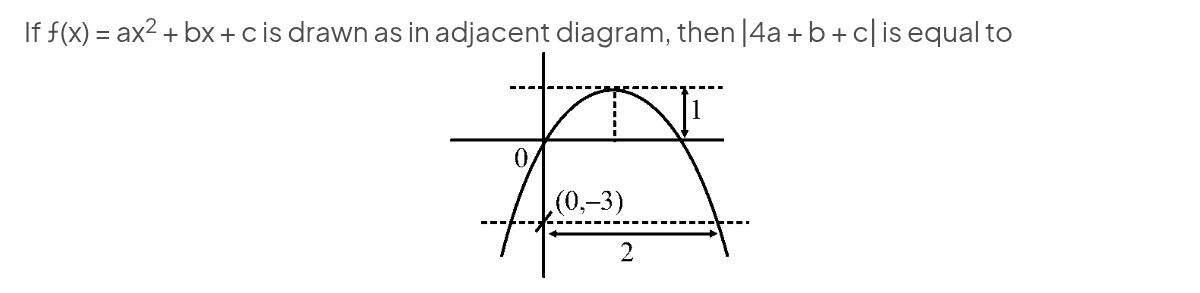
Question: If $f(x) = ax^2 + bx + c$ is drawn as in adjacent diagram, then $|4a + b + c|$ is equal to...
If f(x)=ax2+bx+c is drawn as in adjacent diagram, then ∣4a+b+c∣ is equal to
A
2
B
3
C
5
D
6
Answer
5
Explanation
Solution
The given function is f(x)=ax2+bx+c. From the graph, we can observe the following:
- The y-intercept is at (0,−3). Substituting x=0 into the function, we get f(0)=a(0)2+b(0)+c=c. Thus, c=−3.
- The graph shows that the parabola intersects the line y=−3 at x=0 and at another point to the right of the y-axis. The horizontal distance between these two intersection points is given as 2. To find the x-coordinates where f(x)=−3, we set ax2+bx+c=−3. Substituting c=−3, we have ax2+bx−3=−3, which simplifies to ax2+bx=0. Factoring out x, we get x(ax+b)=0. The solutions are x=0 and x=−ab. Since the horizontal distance between these two points is 2, we have ∣0−(−ab)∣=2, which means ∣ab∣=2. From the diagram, the other intersection point is to the right of x=0, so −ab=2, which implies b=−2a.
- The vertex of the parabola is located at x=−2ab. Substituting b=−2a, we get x=−2a−2a=1. The y-coordinate of the vertex is given as 1 unit above the line y=−3, so the vertex's y-coordinate is −3+1=−2. Substituting the vertex coordinates (1,−2) into the function: f(1)=a(1)2+b(1)+c=a+b+c=−2. We know c=−3 and b=−2a. Substituting these values: a+(−2a)+(−3)=−2 −a−3=−2 −a=1 a=−1. Now we can find b: b=−2a=−2(−1)=2. So, the coefficients are a=−1, b=2, and c=−3. The function is f(x)=−x2+2x−3.
We need to find the value of ∣4a+b+c∣. 4a+b+c=4(−1)+2+(−3)=−4+2−3=−5. ∣4a+b+c∣=∣−5∣=5.
