Question

If

$f(x)= (4 \cos^4 x - 2 \cos^2 x - \frac{1}{2} \cos 4x + 2 \sin^2 x - x^9)^{\frac{1}{9}}$

then the value of $f (f (2))$ is equal to

Answer 1

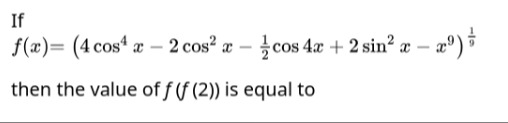
2

Answer 2

To find the value of $f(f(2))$, we first need to simplify the expression for $f(x)$.

The given function is $f(x)= (4 \cos^4 x - 2 \cos^2 x - \frac{1}{2} \cos 4x + 2 \sin^2 x - x^9)^{\frac{1}{9}}$.

Let's simplify the expression inside the parenthesis, $E = 4 \cos^4 x - 2 \cos^2 x - \frac{1}{2} \cos 4x + 2 \sin^2 x - x^9$.

We use the following trigonometric identities:

1. $\cos 2x = 2 \cos^2 x - 1 \implies 2 \cos^2 x = 1 + \cos 2x$
2. $\cos 2x = 1 - 2 \sin^2 x \implies 2 \sin^2 x = 1 - \cos 2x$
3. $\cos 4x = 2 \cos^2 2x - 1$

Now, substitute these into the expression $E$:

• $4 \cos^4 x = (2 \cos^2 x)^2 = (1 + \cos 2x)^2 = 1 + 2 \cos 2x + \cos^2 2x$
• $-2 \cos^2 x = -(1 + \cos 2x) = -1 - \cos 2x$
• $-\frac{1}{2} \cos 4x = -\frac{1}{2} (2 \cos^2 2x - 1) = -\cos^2 2x + \frac{1}{2}$
• $2 \sin^2 x = 1 - \cos 2x$
• $-x^9$ remains as is.

Substitute these simplified terms back into $E$: $E = (1 + 2 \cos 2x + \cos^2 2x) + (-1 - \cos 2x) + (-\cos^2 2x + \frac{1}{2}) + (1 - \cos 2x) - x^9$

Group terms:

• Constant terms: $1 - 1 + \frac{1}{2} + 1 = \frac{3}{2}$
• Terms with $\cos 2x$: $2 \cos 2x - \cos 2x - \cos 2x = 0$
• Terms with $\cos^2 2x$: $\cos^2 2x - \cos^2 2x = 0$
• Term with $x^9$: $-x^9$

So, the expression $E$ simplifies to: $E = \frac{3}{2} - x^9$

Therefore, the function $f(x)$ becomes: $f(x) = \left(\frac{3}{2} - x^9\right)^{\frac{1}{9}}$

Now, we need to find $f(f(2))$. First, calculate $f(2)$: $f(2) = \left(\frac{3}{2} - 2^9\right)^{\frac{1}{9}}$

Let $y = f(2)$. So $y = \left(\frac{3}{2} - 2^9\right)^{\frac{1}{9}}$. We need to find $f(y)$. Substitute $y$ into the simplified $f(x)$: $f(y) = \left(\frac{3}{2} - y^9\right)^{\frac{1}{9}}$

Now, substitute the expression for $y^9$: Since $y = \left(\frac{3}{2} - 2^9\right)^{\frac{1}{9}}$, then $y^9 = \frac{3}{2} - 2^9$.

Substitute this into the expression for $f(y)$: $f(y) = \left(\frac{3}{2} - \left(\frac{3}{2} - 2^9\right)\right)^{\frac{1}{9}}$ $f(y) = \left(\frac{3}{2} - \frac{3}{2} + 2^9\right)^{\frac{1}{9}}$ $f(y) = (2^9)^{\frac{1}{9}}$ $f(y) = 2$

Thus, $f(f(2)) = 2$.