Question

If function $f\left( x \right)=\left[ \dfrac{{{\left( x-2 \right)}^{3}}}{a} \right]\sin \left( x-2 \right)+a\cos \left( x-2 \right)$, $\left[ . \right]$ denotes the greatest function, is continuous in $\left[ 4,6 \right]$, then find the values of $a$.

Answer 1

In this question we have been given an expression which is a combination of the greatest integer function and trigonometric functions. We know that the trigonometric functions will be continuous since trigonometric functions are continuous functions. We will look at the values of $x$ in the domain and then find the value of $a$ such that it satisfies the required solution.

Complete step-by-step solution:
We have the given expression as:
$\Rightarrow f\left( x \right)=\left[ \dfrac{{{\left( x-2 \right)}^{3}}}{a} \right]\sin \left( x-2 \right)+a\cos \left( x-2 \right)$
The function $f\left( x \right)$ is a combination of a greatest integer function and trigonometric functions. We know that trigonometric functions are continuous for all values of $\theta$ by looking at their graphs. The $\sin \theta$ graph looks like:

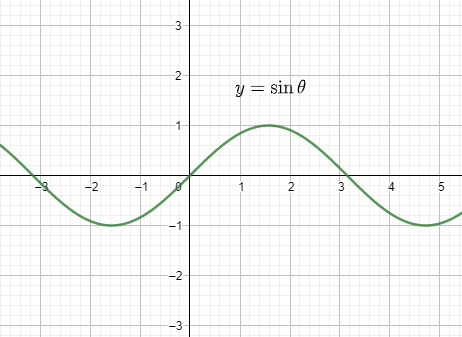
And the graph of $\cos \theta$ looks like:

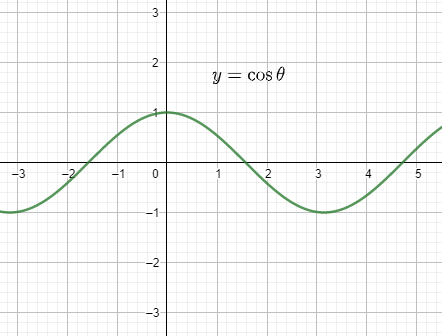
Therefore, we need to find the value of $a$ using the greatest integer function.
We have the greatest integer function given to us as:
$\Rightarrow \left[ \dfrac{{{\left( x-2 \right)}^{2}}}{a} \right]$
We know the greatest integer is discontinuous from its graph which is:

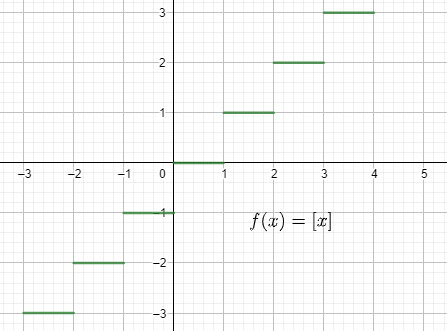
Now in the domain $\left[ 4,6 \right]$ we have the values of the greatest integer function as:
$\Rightarrow \left[ \dfrac{{{\left( 4-2 \right)}^{3}}}{a},\dfrac{{{\left( 6-2 \right)}^{3}}}{a} \right]$
On simplifying, we get:
$\Rightarrow \left[ \dfrac{8}{a},\dfrac{64}{a} \right]$
So, we know that the numerator has the value from $8$ to $64$ and if the greatest integer function has a value greater than $1$ then on multiplying it with the trigonometric function it will yield a non-continuous function.,
This means that the term in the greatest integer function should be lesser than $1$, such that its greatest integer function becomes $0$ and only the continuous part remains.
We know that the value of the numerator can be maximum $64$ in the given domain so, if $a>64$, we will always have a value lesser than $1$ in the greatest integer function.
Therefore, the value of $a>64$. On writing it in the general form, we get:
$a\in \left( 64,\infty \right)$, which is the required solution.

Note: In this question we have used the greatest integer function which gives us the greatest integer less than a real number. For example, the greatest integer function $\left[ 5.5 \right]$ will be $5$. Similar to the greatest integer function, there also exists the least integer function which gives us the least integer greater than a real number. For example, the least integer function $\left[ 5.5 \right]$ will be $6$.